
【题目】平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,过椭圆右焦点
,过椭圆右焦点![]() 作两条互相垂直的弦,当其中一条弦所在直线斜率为0时,两弦长之和为6.
作两条互相垂直的弦,当其中一条弦所在直线斜率为0时,两弦长之和为6.
(1)求椭圆的方程;
(2)![]() 是抛物线
是抛物线![]() :
: ![]() 上两点,且
上两点,且![]() 处的切线相互垂直,直线
处的切线相互垂直,直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,求弦
两点,求弦![]() 的最大值.
的最大值.
科目:高中数学 来源: 题型:
【题目】如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.
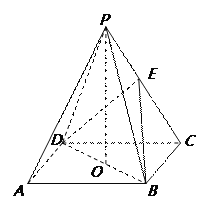
.求证:(Ⅰ)PA∥平面BDE;(Ⅱ)平面PAC⊥平面BDE;(III)若PB与底面所成的角为600, AB=2a,求三棱锥E-BCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有2名老师,3名男生,3名女生站成一排照相留念,在下列情况中,各有多少种不同站法?
(1)3名男生必须站在一起;
(2)2名老师不能相邻;
(3)若3名女生身高都不等,从左到右女生必须由高到矮的顺序站.(最终结果用数字表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设人的某一特征(如眼睛的大小)是由他的一对基因所决定,以d表示显性基因,r表示隐性基因,则具有dd基因的人为纯显性,具有rr基因的人为纯隐性,具有rd基因的人为混合性,纯显性与混合性的人都显露显性基因决定的某一特征,孩子从父母身上各得到一个基因,假定父母都是混合性,问:
(1)1个孩子显露显性特征的概率是多少?
(2)“该父母生的2个孩子中至少有1个显露显性特征”,这种说法正确吗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
, ![]() 为坐标原点,
为坐标原点, ![]() 是双曲线上在第一象限内的点,直线
是双曲线上在第一象限内的点,直线![]() 分别交双曲线
分别交双曲线![]() 左、右支于另一点
左、右支于另一点![]() ,
, ![]() ,且
,且![]() ,则双曲线
,则双曲线![]() 的离心率为( )
的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
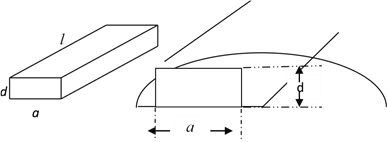
【题目】一根水平放置的长方体形枕木的安全负荷与它的宽度![]() 成正比,与它的厚度
成正比,与它的厚度![]() 的平方成正比,与它的长度
的平方成正比,与它的长度![]() 的平方成反比.
的平方成反比.
(Ⅰ)将此枕木翻转90°(即宽度变为厚度),枕木的安全负荷会如何变化?为什么?(设翻转前后枕木的安全负荷分别为![]() 且翻转前后的比例系数相同都为
且翻转前后的比例系数相同都为![]() )
)
(Ⅱ)现有一根横断面为半圆(已知半圆的半径为![]() )的木材,用它来截取成长方体形的枕木,其长度为10,问截取枕木的厚度为
)的木材,用它来截取成长方体形的枕木,其长度为10,问截取枕木的厚度为![]() 多少时,可使安全负荷
多少时,可使安全负荷![]() 最大?
最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
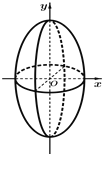
【题目】(2017届高三第二次湖北八校文数试卷第16题)祖暅(公元前5~6世纪)是我国齐梁时代的数学家,是祖冲之的儿子.他提出了一条原理:“幂势既同,则积不容异.”这里的“幂”指水平截面的面积,“势”指高.这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体体积相等.设由椭圆![]() 所围成的平面图形绕
所围成的平面图形绕![]() 轴旋转一周后,得一橄榄状的几何体
轴旋转一周后,得一橄榄状的几何体
(如图)(称为椭球体),课本中介绍了应用祖暅原理求球体体积公式的做法,请类比此法,求出椭球体体积,其体积等于______ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com