
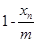 的乘积成正比,比例系数为
的乘积成正比,比例系数为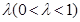 ,其中m是与n无关的常数,且x1<m,
,其中m是与n无关的常数,且x1<m,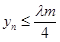 ;
; 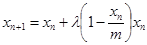 ,证明用数学归纳法,过程详见解析.
,证明用数学归纳法,过程详见解析.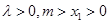 就可证明
就可证明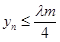 ;(2)由已知有该年的增长量
;(2)由已知有该年的增长量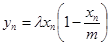 ,所以第n+1年年初的的数量xn+1=xn+yn,代入即可用 xn表示xn+1;证明草原上的野兔总数量恒小于m,即证对一切非零自然数n,都有xn<m,可考虑用数学归纳法来证明:当n=1时显然成立;再假设当
,所以第n+1年年初的的数量xn+1=xn+yn,代入即可用 xn表示xn+1;证明草原上的野兔总数量恒小于m,即证对一切非零自然数n,都有xn<m,可考虑用数学归纳法来证明:当n=1时显然成立;再假设当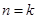 时,命题成立,则对n=k+1时,由于
时,命题成立,则对n=k+1时,由于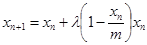 是xk的一个二次函数,结合二次函数的性质,可证
是xk的一个二次函数,结合二次函数的性质,可证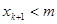 成立,从而有对一切正整数n,
成立,从而有对一切正整数n,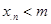 ,即是草原上的野兔总数量恒小于m.
,即是草原上的野兔总数量恒小于m.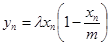 ,配方得:
,配方得: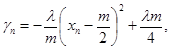 ∵
∵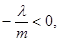 ∴当且仅当
∴当且仅当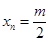 时,
时,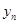 取得最大值
取得最大值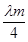 ,即
,即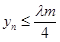 (5分)
(5分) 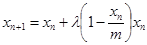 (8分)
(8分)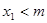 ,故命题成立
,故命题成立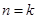 时,命题成立
时,命题成立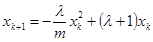 是xk的一个二次函数
是xk的一个二次函数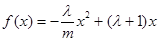 ,
,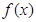 有对称轴
有对称轴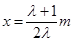 ,开口向下,由
,开口向下,由 ,则
,则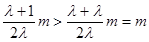 ,于是在
,于是在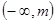 上均有
上均有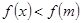 =m
=m ,即知
,即知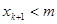 ,∴当
,∴当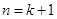 时,命题成立,综上知,对一切正整数n,
时,命题成立,综上知,对一切正整数n,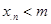 这就是说该草原上的野兔数量不可能无限增长 (13分)
这就是说该草原上的野兔数量不可能无限增长 (13分)

科目:高中数学 来源:不详 题型:解答题
 )
)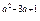 的单调递减区间.
的单调递减区间.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
|
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
|
| A.2 | B.16 | C.2或16 | D.-2或16 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
|
| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com