
【题目】已知函数 ![]() ,把方程f(x)=x的根按从小到大的顺序排列成一个数列,则该数列的通项公式为( )
,把方程f(x)=x的根按从小到大的顺序排列成一个数列,则该数列的通项公式为( )
A.![]() (n∈N*)
(n∈N*)
B.an=n(n﹣1)(n∈N*)
C.an=n﹣1(n∈N*)
D.an=2n﹣2(n∈N*)
【答案】C
【解析】解:若0<x≤1,则﹣1<x﹣1<0,得f(x)=f(x﹣1)+1=2x﹣1 , 若1<x≤2,则0<x﹣1≤1,得f(x)=f(x﹣1)+1=2x﹣2+1
若2<x≤3,则1<x﹣1≤2,得f(x)=f(x﹣1)+1=2x﹣3+2
若3<x≤4,则2<x﹣1<3,得f(x)=f(x﹣1)+1=2x﹣4+3
以此类推,若n<x≤n+1(其中n∈N),则f(x)=f(x﹣1)+1=2x﹣n﹣1+n,
下面分析函数f(x)=2x的图象与直线y=x+1的交点
很显然,它们有两个交点(0,1)和(1,2),
由于指数函数f(x)=2x为增函数且图象下凸,故它们只有这两个交点.
然后①将函数f(x)=2x和y=x+1的图象同时向下平移一个单位即得到函数f(x)=2x﹣1和y=x的图象,
取x≤0的部分,可见它们有且仅有一个交点(0,0).
即当x≤0时,方程f(x)﹣x=0有且仅有一个根x=0.
②取①中函数f(x)=2x﹣1和y=x图象﹣1<x≤0的部分,再同时向上和向右各平移一个单位,
即得f(x)=2x﹣1和y=x在0<x≤1上的图象,显然,此时它们仍然只有一个交点(1,1).
即当0<x≤1时,方程f(x)﹣x=0有且仅有一个根x=1.
③取②中函数f(x)=2x﹣1和y=x在0<x≤1上的图象,继续按照上述步骤进行,
即得到f(x)=2x﹣2+1和y=x在1<x≤2上的图象,显然,此时它们仍然只有一个交点(2,2).
即当1<x≤2时,方程f(x)﹣x=0有且仅有一个根x=2.
④以此类推,函数y=f(x)与y=x在(2,3],(3,4],…(n,n+1]上的交点依次为(3,3),(4,4),…(n+1,n+1).
即方程f(x)﹣x=0在(2,3],(3,4],…(n,n+1]上的根依次为3,4,…n+1.
综上所述方程f(x)﹣x=0的根按从小到大的顺序排列所得数列为
0,1,2,3,4,…
其通项公式为an=n﹣1;
故选C.
【考点精析】本题主要考查了数列的通项公式的相关知识点,需要掌握如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 已知2Sn=3n+3.
(Ⅰ)求{an}的通项公式;
(Ⅱ)若数列{bn},满足anbn=log3an , 求{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)= ![]() (x∈R)且x≠﹣1,g(x)=x2+2(x∈R).
(x∈R)且x≠﹣1,g(x)=x2+2(x∈R).
(1)求f(2),g(2)的值;
(2)求f[g(2)]的值;
(3)求f[g(x)]和g[f(x)]的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
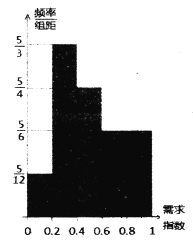
【题目】某公司每个工作日由位于市区的总公司向位于郊区的分公司开一个来回的班车(每年按200个工作日计算),现有两种使用班车的方案,方案一是购买一辆大巴,需花费90万元,报废期为10年,车辆平均每年的各种费用合计5万元,司机年工资6万元,司机每天请假的概率为0.1(每年请假时间不超过15天不扣工资,超过15天每天100元),若司机请假则需从公交公司雇佣司机,每天支付300元工资.方案二是租用公交公司的车辆(含司机),根据调研每年12个月的车辆需求指数如直方图所示,其中当某月车辆需求指数在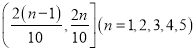 时,月租金为
时,月租金为![]() 万元.
万元.
(1)若购买大巴,设司机每年请假天数为![]() ,求公司因司机请假而增加的花费
,求公司因司机请假而增加的花费![]() (元)及使用班车年平均花费
(元)及使用班车年平均花费![]() (万元)的数学期望
(万元)的数学期望![]() .
.
(2)试用调研数据,给出公司使用班车的建议,使得年平均花费最少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=x+ ![]() (a>0)在区间
(a>0)在区间 ![]() 上单调递减,在区间
上单调递减,在区间 ![]() 上单调递增;函数
上单调递增;函数 ![]()
(1)请写出函数f(x)=x2+ ![]() (a>0)与函数g(x)=xn+
(a>0)与函数g(x)=xn+ ![]() (a>0,n∈N,n≥3)在(0,+∞)的单调区间(只写结论,不证明);
(a>0,n∈N,n≥3)在(0,+∞)的单调区间(只写结论,不证明);
(2)求函数h(x)的最值;
(3)讨论方程h2(x)﹣3mh(x)+2m2=0(0<m≤30)实根的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)是R上的偶函数,对于任意x∈R,都有f(x+6)=f(x)+f(3)成立,当x1 , x2∈[0,3],且x1≠x2时,都有 ![]() .给出下列命题: ①f(3)=0;
.给出下列命题: ①f(3)=0;
②直线x=﹣6是函数y=f(x)的图象的一条对称轴;
③函数y=f(x)在[﹣9,﹣6]上为增函数;
④函数y=f(x)在[﹣9,9]上有四个零点.
其中所有正确命题的序号为(把所有正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= 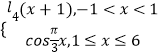 ,若存在实数x1 , x2 , x3 , x4 , 满足x1<x2<x3<x4 , 且f(x1)=f(x2)=f(x3)=f(x4),则
,若存在实数x1 , x2 , x3 , x4 , 满足x1<x2<x3<x4 , 且f(x1)=f(x2)=f(x3)=f(x4),则 ![]() 的取值范围是( ).
的取值范围是( ).
A.(0,4)
B.(0, ![]() )
)
C.( ![]() ,
, ![]() )
)
D.( ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在五面体ABCDEF中,四边形ABCD是边长为2的正方形,EF∥平面ABCD,EF=1,FB=FC,∠BFC=90°,AE= ![]() ,H是BC的中点.
,H是BC的中点. 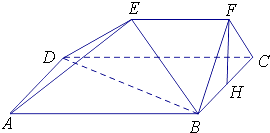
(1)求证:FH∥平面BDE;
(2)求证:AB⊥平面BCF;
(3)求五面体ABCDEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)是定义在R上的偶函数,且对任意的x∈R恒有f(x+1)=f(x-1),
已知当x∈[0,1]时f(x)=(![]() )1-x,则
)1-x,则
①2是函数f(x)的周期;
②函数f(x)在(1,2)上是减函数,在(2,3)上是增函数;
③函数f(x)的最大值是1,最小值是0;
④当x∈(3,4)时,f(x)=(![]() )x-3.
)x-3.
其中所有正确命题的序号是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com