练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．已知函数f（x）的定义域为[0，2]，则函数f（x-3）的定义域为（　　）
    A．[-3，-1]B．[0，2]C．[2，5]D．[3，5]

    分析 利用复合函数的定义求法直接由0≤x-3≤2，即可得函数f（x-3）的定义域．

    解答 解：因为函数f（x）的定义域为[0，2]，
    所以0≤x≤2，由0≤x-3≤2，得3≤x≤5，
    即函数的定义域为[3，5]，
    故选：D．

    点评 本题主要考查复合函数的定义域的求法，直接代入即可求复合函数的定义域．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    16．已知平面向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为120°，|$\overrightarrow{a}$|=2，|$\overrightarrow{b}$|=1，则|$\overrightarrow{a}$+2$\overrightarrow{b}$|=（　　）
    A．2B．$\sqrt{6}$C．2$\sqrt{3}$D．$\sqrt{10}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

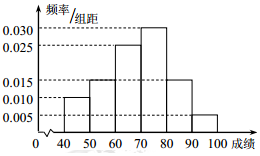    9．在某校举行的航天知识竞赛中，参与竞赛的文科生与理科生人数之比为1：3，且成绩分布在[40，100]，分数在80以上（含80）的同学获奖．按文理科用分层抽样的方法抽取200人的成绩作为样本，得到成绩的频率分布直方图（见图）．
    （1）求a的值，并计算所抽取样本的平均值$\overline x$（同一组中的数据用该组区间的中点值作代表）；
    （2）填写下面的2×2列联表，能否有超过95%的把握认为“获奖与学生的文理科有关”？
    文科生理科生合计
    获奖5
    不获奖
    合计200
    附表及公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d
    P（K2≥k）0.150.100.050.0250.0100.0050.001
    k2.0722.7063.8415.0246.6357.87910.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

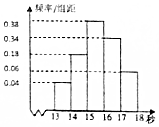    6．为调查运城市学生百米运动成绩，从该市学生中按照男女比例随机抽取50名学生进行百米测试，学生成绩全部都介于13秒到18秒之间，将测试结果按如下方式分成五组，第一组[13，14），第二组[14，15）…第五组[17，18]，如图是按上述分组方法得到的频率分布直方图．
    （Ⅰ）求这组数据的中位数（精确到0.1）
    （Ⅱ）根据有关规定，成绩小于16秒为达标．如果男女生使用相同的达标标准，则男女生达标情况如表：
    性别
    是否达标    		男女合计
    达标a=24b=630
    不达标c=8d=1220
    合计3218
    根据表中所给的数据，能否有99%的把握认为“体育达标与性别有关”？若有，你能否提出一个更好的解决方法来？
    附：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
    P（K2≥K）0.0500.0100.001
    K3.8416.62510.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知函数f（x）=2$\sqrt{3}$sin2x+4cos2x-3
    （1）求f（x）的单调递增区间；
    （2）在△ABC中，a、b、c分别为内角A、B、C所对的边，且对x∈R，f（x）的最大值为f（A），若a=2，求$\overrightarrow{AB}$•$\overrightarrow{AC}$的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

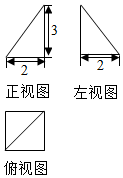    3．已知某个几何体的三视图如图所示，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是（　　）
    A．$\frac{4}{3}$cm3B．$\frac{8}{3}$cm3C．2cm3D．4cm3

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知全集U=R，集合A={x|0＜log2x＜2}，B={x|x≤3m-4或x≥8+m}（m＜6）．
    （1）若m=2，求A∩（∁UB）；
    （2）若A∩（∁UB）=∅，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．若x∈（1，+∞），则y=2x+$\frac{1}{x-1}$的最小值是2$\sqrt{2}$+2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

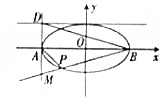    8．如图，椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右顶点分别为A，B，离心率为$\frac{\sqrt{2}}{2}$，直线x=-a与y=b交于点D，且|BD|=3$\sqrt{2}$，过点B作直线l交直线x=-a于点M，交椭圆于另一点P．
    （1）求直线MB与直线PA的斜率之积；
    （2）证明：$\overrightarrow{OM}$•$\overrightarrow{OP}$为定值．

    查看答案和解析>>

    同步练习册答案