
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c.满足2acosC+bcosC+ccosB=0.
(Ⅰ)求角C的大小;
(Ⅱ)若a=2,△ABC的面积为![]() ,求C的大小。
,求C的大小。
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)先根据正弦定理将边化为角,再根据诱导公式化简得cosC=-![]() ,即得角C的大小;(2)先根据三角形面积公式得b,再根据余弦定理得c.
,即得角C的大小;(2)先根据三角形面积公式得b,再根据余弦定理得c.
试题解析:解:(I)在△ABC中,∵2acosC+bcosC+ccosB=0,
∴由正弦定理可得:2sinAcosC+sinBcosC+sinCcosB=0,
∴2sinAcosC+sin(B+C)=0,..
又△ABC中,sin(B+C)=sinA≠0.∴cosC=-![]() ,.
,.
∵0<C< ![]() .∴C=
.∴C=![]() ...
...
(II)由S=![]() absinC=
absinC=![]() ,a=2,C=
,a=2,C=![]() 得b=1.
得b=1.
由余弦定理得c![]() =4+1-2×2×1×(-
=4+1-2×2×1×(-![]() )=7,∴c=
)=7,∴c=![]()


科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,曲线
,曲线![]() ,且
,且![]() 与
与![]() 的焦点之间的距离为
的焦点之间的距离为![]() ,且
,且![]() 与
与![]() 在第一象限的交点为
在第一象限的交点为![]() .
.
(1)求曲线![]() 的方程和点
的方程和点![]() 的坐标;
的坐标;
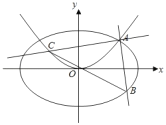
(2)若过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,过点
,过点![]() 与
与![]() 垂直的直线与
垂直的直线与![]() 的另一个交点为
的另一个交点为![]() .设
.设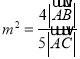 ,试求
,试求![]() 取值范围.
取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在贯彻中共中央国务院关于精准扶贫政策的过程中,某单位定点帮扶甲、乙两个村各50户贫困户.为了做到精准帮扶,工作组对这100户村民的年收入情况、劳动能力情况、子女受教育情况、危旧房情况、患病情况等进行调查,并把调查结果转化为各户的贫困指标![]() 和
和![]() ,制成下图,其中“
,制成下图,其中“![]() ”表示甲村贫困户,“
”表示甲村贫困户,“![]() ”表示乙村贫困户.若
”表示乙村贫困户.若![]() ,则认定该户为“绝对贫困户”,若
,则认定该户为“绝对贫困户”,若![]() ,则认定该户为“相对贫困户”,若
,则认定该户为“相对贫困户”,若![]() ,则认定该户为“低收入户”;若
,则认定该户为“低收入户”;若![]() ,则认定该户为“今年能脱贫户”,否则为“今年不能脱贫户”.
,则认定该户为“今年能脱贫户”,否则为“今年不能脱贫户”.
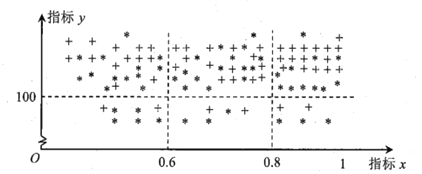
(1)从乙村的50户中随机选出一户,求该户为“绝对贫困户”的概率;
(2)从甲村所有“今年不能脱贫的非绝对贫困户”中任选2户,求选出的2户均为“低收入户”的概率;
(3)试比较这100户中,甲、乙两村指标![]() 的方差的大小(只需写出结论).
的方差的大小(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为![]() 的函数
的函数![]() 是奇函数.
是奇函数.
(1) 求实数![]() 的值;
的值;
(2) 判断并用定义证明该函数在定义域![]() 上的单调性;
上的单调性;
(3) 若方程![]() 在
在![]() 内有解,求实数
内有解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有以下判断:①![]() 与
与![]() 表示同一函数;②函数
表示同一函数;②函数![]() 的图像与直线
的图像与直线![]() 最多有一个交点;③
最多有一个交点;③![]() 不是函数;④若点
不是函数;④若点![]() 在
在![]() 的图像上,则函数
的图像上,则函数![]() 的图像必过点
的图像必过点![]() .其中正确的判断有___________.
.其中正确的判断有___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABCA1B1C1中,BC=BB1,∠BAC=∠BCA=![]() ∠ABC,点E是A1B与AB1的交点,点D在线段AC上,B1C∥平面A1BD.
∠ABC,点E是A1B与AB1的交点,点D在线段AC上,B1C∥平面A1BD.
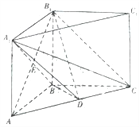
(1)求证:BD⊥A1C;
(2)求证:AB1⊥平面A1BC。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内两点![]() .
.
(1)求![]() 的中垂线方程;
的中垂线方程;
(2)求过![]() 点且与直线
点且与直线![]() 平行的直线
平行的直线![]() 的方程;
的方程;
(3)一束光线从![]() 点射向(2)中的直线
点射向(2)中的直线![]() ,若反射光线过点
,若反射光线过点![]() ,求反射光线所在的直线方程.
,求反射光线所在的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国务院批准从2009年起,将每年8月8日设置为“全民健身日”,为响应国家号召,各地利用已有土地资源建设健身场所.如图,有一个长方形地块![]() ,边
,边![]() 为
为![]() ,
,![]() 为
为![]() .地块的一角是草坪(图中阴影部分),其边缘线
.地块的一角是草坪(图中阴影部分),其边缘线![]() 是以直线
是以直线![]() 为对称轴,以
为对称轴,以![]() 为顶点的抛物线的一部分.现要铺设一条过边缘线
为顶点的抛物线的一部分.现要铺设一条过边缘线![]() 上一点
上一点![]() 的直线型隔离带
的直线型隔离带![]() ,
,![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上(隔离带不能穿越草坪,且占地面积忽略不计),将隔离出的
上(隔离带不能穿越草坪,且占地面积忽略不计),将隔离出的![]() 作为健身场所.则
作为健身场所.则![]() 的面积为
的面积为![]() 的最大值为____________(单位:
的最大值为____________(单位:![]() ).
).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com