
【题目】下列命题正确的是( )
A.已知随机变量![]() ,若
,若![]() .则
.则![]()
B.已知分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 的观察值为
的观察值为![]() ,则当
,则当![]() 的值越大时,“
的值越大时,“![]() 与
与![]() 有关”的可信度越小.
有关”的可信度越小.
C.在线性回归模型中,计算其相关指数![]() ,则可以理解为:解析变量对预报变量的贡献率约为
,则可以理解为:解析变量对预报变量的贡献率约为![]()
D.若对于变量![]() 与
与![]() 的
的![]() 组统计数据的线性回归模型中,相关指数
组统计数据的线性回归模型中,相关指数![]() .又知残差平方和为
.又知残差平方和为![]() .那么
.那么![]() .(注意:
.(注意: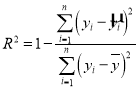 )
)
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,![]() 是正方形ABCD的外接圆,点P在劣弧AB上(P不与A、B重合),DP分别交AO、AB于点Q、T,
是正方形ABCD的外接圆,点P在劣弧AB上(P不与A、B重合),DP分别交AO、AB于点Q、T, ![]() 在点P处的切线交DA的延长线于点E,劣弧BC的中点为F.
在点P处的切线交DA的延长线于点E,劣弧BC的中点为F.

(1)问:何时F、T、E三点共线?请说明理由.
(2)求比值![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县共有90间农村淘宝服务站,随机抽取5间,统计元旦期间的网购金额(单位:万元)的茎叶图如图所示,其中茎为十位数,叶为个位数.若网购金额(单位:万元)不小于18的服务站定义为优秀服务站,其余为非优秀服务站.从随机抽取的5间服务站中再任取2间作网购商品的调查,则恰有1间是优秀服务站的概率为_____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,P,Q分别为棱BC和棱CC1的中点,则下列说法正确的是( )
A.BC1//平面AQP
B.平面APQ截正方体所得截面为等腰梯形
C.A1D⊥平面AQP
D.异面直线QP与A1C1所成的角为60°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以椭圆的2个焦点与1个短轴端点为顶点的三角形的面积为2
,以椭圆的2个焦点与1个短轴端点为顶点的三角形的面积为2![]() 。
。
(1)求椭圆的方程;
(2)如图,斜率为k的直线l过椭圆的右焦点F,且与椭圆交与A,B两点,以线段AB为直径的圆截直线x=1所得的弦的长度为![]() ,求直线l的方程。
,求直线l的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年1月10日,引发新冠肺炎疫情的COVID-9病毒基因序列公布后,科学家们便开始了病毒疫苗的研究过程.但是类似这种病毒疫苗的研制需要科学的流程,不是一朝一夕能完成的,其中有一步就是做动物试验.已知一个科研团队用小白鼠做接种试验,检测接种疫苗后是否出现抗体.试验设计是:每天接种一次,3天为一个接种周期.已知小白鼠接种后当天出现抗体的概率为![]() ,假设每次接种后当天是否出现抗体与上次接种无关.
,假设每次接种后当天是否出现抗体与上次接种无关.
(1)求一个接种周期内出现抗体次数![]() 的分布列;
的分布列;
(2)已知每天接种一次花费100元,现有以下两种试验方案:
①若在一个接种周期内连续2次出现抗体即终止本周期试验,进行下一接种周期,试验持续三个接种周期,设此种试验方式的花费为![]() 元;
元;
②若在一个接种周期内出现2次或3次抗体,该周期结束后终止试验,已知试验至多持续三个接种周期,设此种试验方式的花费为![]() 元.
元.
比较随机变量![]() 和
和![]() 的数学期望的大小.
的数学期望的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com