
【题目】设向量 ![]() =(
=( ![]() sinx,sinx),
sinx,sinx), ![]() =(cosx,sinx),x∈[0,
=(cosx,sinx),x∈[0, ![]() ].
].
(1)若| ![]() |=|
|=| ![]() |,求x的值;
|,求x的值;
(2)设函数f(x)= ![]()
![]() ,求f(x)的最大值及单调递增区间.
,求f(x)的最大值及单调递增区间.
【答案】
(1)解:依题意知3sin2x+sin2x=cos2x+sin2x=1
∴sin2x= ![]() ,
,
∵x∈[0, ![]() ].
].
∴sinx= ![]() ,
,
x= ![]() .
.
(2)解:f(x)= ![]()
![]() =
= ![]() sinxcosx+sin2x=
sinxcosx+sin2x= ![]() sin2x﹣
sin2x﹣ ![]() cos2x+
cos2x+ ![]() =sin(2x﹣
=sin(2x﹣ ![]() )+
)+ ![]() ,
,
f(x)max=1+ ![]() =
= ![]() ,
,
由2kπ﹣ ![]() ≤2x﹣
≤2x﹣ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,得kπ﹣
,k∈Z,得kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,
,
∴函数的单调增区间为[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
【解析】(1)先根据题意分别表示出两向量的模,取得sinx的值,进而求得x.(2)表示出函数f(x)的表达式,进而利用二倍角公式和两角和公式化简,进而根据三角函数的图象和性质求得函数的最大值和单调增区间.


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:
【题目】已知命题p:x1 , x2是方程x2﹣mx﹣1=0的两个实根,且不等式a2+4a﹣3≤|x1﹣x2|对任意m∈R恒成立;命题q:不等式x2+2x+a<0有解,若命题p∨q为真,p∧q为假,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015男篮亚锦赛决赛阶段,中国男篮以![]() 连胜的不败成绩赢得第
连胜的不败成绩赢得第![]() 届亚锦赛冠军,同时拿到亚洲唯一
届亚锦赛冠军,同时拿到亚洲唯一![]() 张直通里约奥运会的入场券.赛后,中国男篮主力易建联荣膺本届亚锦赛
张直通里约奥运会的入场券.赛后,中国男篮主力易建联荣膺本届亚锦赛![]() (最有价值球员),下表是易建联在这
(最有价值球员),下表是易建联在这![]() 场比赛中投篮的统计数据.
场比赛中投篮的统计数据.
比分 | 易建联技术统计 | |||
投篮命中 | 罚球命中 | 全场得分 | 真实得分率 | |
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
注:(1)表中![]() 表示出手
表示出手![]() 次命中
次命中![]() 次;
次;
(2)![]() (真实得分率)是衡量球员进攻的效率,其计算公式为:
(真实得分率)是衡量球员进攻的效率,其计算公式为:
![]()
(1)从上述![]() 场比赛中随机选择一场,求易建联在该场比赛中
场比赛中随机选择一场,求易建联在该场比赛中![]() 超过
超过![]() 的概率;
的概率;
(2)我们把比分分差不超过![]() 分的比赛称为“胶着比赛”.为了考验求易建联在“胶着比赛”中的发挥情况,从“胶着比赛”中随机选择两场,求易建联在这两场比赛中
分的比赛称为“胶着比赛”.为了考验求易建联在“胶着比赛”中的发挥情况,从“胶着比赛”中随机选择两场,求易建联在这两场比赛中![]() 至少有一场超过
至少有一场超过![]() 的概率;
的概率;
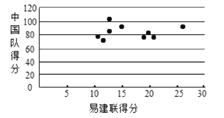
(3)用![]() 来表示易建联某场的得分,用
来表示易建联某场的得分,用![]() 来表示中国队该场的总分,画出散点图如图所示,请根据散点图判断
来表示中国队该场的总分,画出散点图如图所示,请根据散点图判断![]() 与
与![]() 之间是否具有线性相关关系?结合实际简单说明理由.
之间是否具有线性相关关系?结合实际简单说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=sinx的图象上所有的点向右平行移动 ![]() 个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是( )
个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是( )
A.y=sin(2x﹣ ![]() )
)
B.y=sin(2x+ ![]() )
)
C.y=sin( ![]() x﹣
x﹣ ![]() )
)
D.y=sin( ![]() x﹣
x﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(2,﹣3),
=(2,﹣3), ![]() =(﹣5,4),
=(﹣5,4), ![]() =(1﹣λ,3λ+2).
=(1﹣λ,3λ+2).
(1)若△ABC为直角三角形,且∠B为直角,求实数λ的值;
(2)若点A、B、C能构成三角形,求实数λ应满足的条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() +
+ ![]() ,则下列命题中正确命题的序号是 .
,则下列命题中正确命题的序号是 .
①f(x)是偶函数;
②f(x)的值域是[ ![]() ,2];
,2];
③当x∈[0, ![]() ]时,f(x)单调递增;
]时,f(x)单调递增;
④当且仅当x=2kπ± ![]() (k∈Z)时,f(x)=
(k∈Z)时,f(x)= ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.
(Ⅰ) 求证:PC⊥AD;
(Ⅱ) 在棱PB上是否存在一点Q,使得A,Q,M,D四点共面?若存在,指出点Q的位置并证明;若不存在,请说明理由;
(Ⅲ) 求点D到平面PAM的距离. 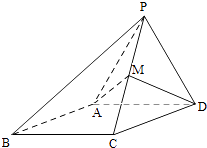
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,直线![]() 经过点
经过点![]() ,倾斜角为
,倾斜角为![]() .在以原点为极点,
.在以原点为极点, ![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的方程为
的方程为![]() .
.
(1)写出直线![]() 的参数方程和曲线
的参数方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com