练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图1-3-2,已知在△ABC中,AB =AC,∠A =36°,BD是∠ABC的平分线,试利用三角形相似的关系说明AD2=DC·AC.

    图1-3-2

    思路解析:有一个角是36°的等腰三角形,它的底角是72°,而BD是底角的平分线,?

    ∴∠CBD=36°,则可推出△ABC∽△BCD,进而由相似三角形对应边成比例推出线段之间的比例关系.

    证明:∵∠A=36°,AB=AC,?

    ∴∠ABC=∠C=72°.?

    又∵BD平分∠ABC，?

    ∴∠ABD=∠CBD=36°.?

    ∴AD =BD =BC，且△ABC∽△BCD.?

    ∴BC∶AB =CD∶BC.?

    ∴BC2=AB·CD.?

    ∴AD2=AC·CD.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：044

    如图1-3-16,已知Rt△ABC中,D是斜边AB的中点,DE⊥AB于D,交AC于F,交BC延长线于E,BG⊥BA,交DC延长线于H,交AC延长线于G.?

    图1-3-16

    求证:(1)GH·CE =DF·BC;?

    (2)DC2=DF·DE;?

    (3)CH·CD =GH·DE;?

    (4)GB∶BA =CH∶BH;?

    (5)CH·EF =BA·DF.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本小题满分14分）如图9-3，已知：射线OA为y=kx(k>0，x>0)，射线OB为y= －kx(x>0)，动点P(x，y)在∠AOx的内部，PM⊥OA于M，PN⊥OB于N，四边形ONPM的面积恰为k.

       （1）当k为定值时，动点P的纵坐标y是横坐标x的函数，求这个函数y=f(x)的解析式；

       （2）根据k的取值范围，确定y=f(x)的定义域.

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年河北省高三第三次考试理科数学 题型：解答题

    （本小题满分12分）

    如图8—3，已知ΔOFQ的面积为S，且．（1）若，求向量与的夹角θ的取值范围；（2）设，，若以O为中心，F为焦点的椭圆经过点Q，当取得最小值时，求此椭圆方程．

     

     

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

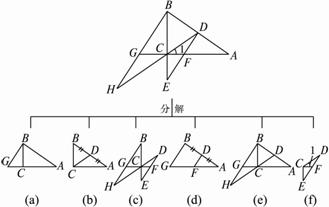
    如图1-3-16,已知Rt△ABC中,D是斜边AB的中点,DE⊥AB于D,交AC于F,交BC延长线于E,BG⊥BA,交DC延长线于H,交AC延长线于G.

    图1-3-16

    求证:(1)GH·CE =DF·BC;

    (2)DC2=DF·DE;

    (3)CH·CD =GH·DE;

    (4)GB∶BA =CH∶BH;

    (5)CH·EF =BA·DF.

    查看答案和解析>>

    同步练习册答案