
【题目】已知抛物线![]() 顶点在原点,焦点在
顶点在原点,焦点在![]() 轴上,抛物线
轴上,抛物线![]() 上一点
上一点![]() 到焦点的距离为3,线段
到焦点的距离为3,线段![]() 的两端点
的两端点![]() ,
, ![]() 在抛物线
在抛物线![]() 上.
上.
(1)求抛物线![]() 的方程;
的方程;
(2)若![]() 轴上存在一点
轴上存在一点![]() ,使线段
,使线段![]() 经过点
经过点![]() 时,以
时,以![]() 为直径的圆经过原点,求
为直径的圆经过原点,求![]() 的值;
的值;
(3)在抛物线![]() 上存在点
上存在点![]() ,满足
,满足![]() ,若
,若![]() 是以角
是以角![]() 为直角的等腰直角三角形,求
为直角的等腰直角三角形,求![]() 面积的最小值.
面积的最小值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)最小值为16.
;(3)最小值为16.
【解析】试题分析:(1)根据抛物线的定义,丨QF丨=丨QQ1丨,即可求得p的值,即可求得抛物线方程;
(2)设AB的方程,代入椭圆方程,由![]() ,根据向量数量积的坐标运算及韦达定理,即可求得m的值;
,根据向量数量积的坐标运算及韦达定理,即可求得m的值;
(3)设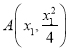 ,
, 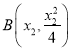 ,
,  ,根据抛物线关于
,根据抛物线关于![]() 轴对称,取
轴对称,取![]() ,记
,记![]() ,
, ![]() ,则有
,则有![]() ,
, ![]() ,所以
,所以![]() ,
, ![]() ,
, ![]() ,由
,由![]() ,即
,即![]() ,进而化简求出
,进而化简求出![]() ,得:
,得: ![]() ,
,  ,即可求得△ABD面积的最小值.
,即可求得△ABD面积的最小值.
试题解析:
(1)设抛物线的方程为![]() ,抛物线的焦点为
,抛物线的焦点为![]() ,则
,则![]() ,所以
,所以![]() ,
,
则抛物线![]() 的方程为
的方程为![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,要使以
,要使以![]() 为直径的圆经过原点,则只需
为直径的圆经过原点,则只需![]() 即可,
即可,
联立方程![]()
![]() ,则
,则![]() ,
, ![]() ,
,
![]()
![]() ,
,
解得: ![]() .
.
(3)如图所示,
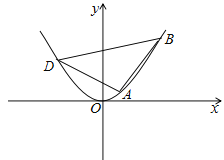
设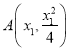 ,
, 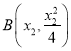 ,
, 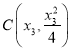 ,根据抛物线关于
,根据抛物线关于![]() 轴对称,取
轴对称,取![]() ,记
,记![]() ,
, ![]() ,
,
则有![]() ,
, ![]() ,所以
,所以![]() ,
, ![]() ,
, ![]() ,
,
又因为![]() 是以
是以![]() 为顶点的等腰直角三角形,所以
为顶点的等腰直角三角形,所以![]() ,
,
即![]() ,将
,将![]() 代入得:
代入得:
![]()
进而化简求出![]() ,得:
,得: ![]() ,
,
则 ,可以先求
,可以先求![]() 的最小值即可,
的最小值即可,
![]() ,令
,令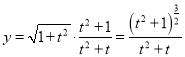 ,
,
则
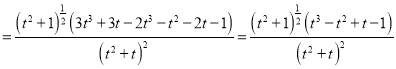
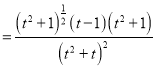 ,
,
所以可以得出当![]() 即
即![]() 时,
时, ![]() 最小值为
最小值为![]() ,此时
,此时![]() ,
,
即当![]() ,
, ![]() ,
, ![]() 时,
时, ![]() 为等腰直角三角形,且此时面积最小,最小值为16.
为等腰直角三角形,且此时面积最小,最小值为16.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为了得到函数y=sin(2x﹣ ![]() )的图象,只需把函数y=sin2x的图象上所有的点( )
)的图象,只需把函数y=sin2x的图象上所有的点( )
A.向左平移 ![]() 个单位长度
个单位长度
B.向右平移 ![]() 个单位长度
个单位长度
C.向左平移 ![]() 个单位长度
个单位长度
D.向右平移 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 在区间
在区间![]() 上的最大值和最小值;
上的最大值和最小值;
(2)若在区间![]() 上, 函数
上, 函数![]() 的图象恒在直线
的图象恒在直线![]() 下方, 求
下方, 求![]() 的取值范围;
的取值范围;
(3)设![]() .当
.当![]() 时, 若对于任意
时, 若对于任意![]() ,存在
,存在![]() ,使
,使![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() (
(![]() ),原点
),原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,其中:点
,其中:点![]() ,点
,点![]() .
.
(1)求该椭圆![]() 的离心率
的离心率![]() ;
;
(2)经过椭圆右焦点![]() 的直线
的直线![]() 和该椭圆交于
和该椭圆交于![]() 两点,点
两点,点![]() 在椭圆上,
在椭圆上, ![]() 为原点,若
为原点,若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两千多年前,古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题.他们在沙滩上画点或用小石子表示数,按照点或小石子能排列的形状对数进行分类.如下图中实心点的个数5,9,14,20,…为梯形数.根据图形的构成,记此数列的第2013项为a2013 , 则a2013﹣5=( ) 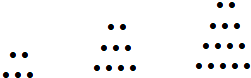
A.2019×2013
B.2019×2012
C.1006×2013
D.2019×1006
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体A1B1C1D1﹣ABCD中,AD=CD=4,AD1=5,M是线段B1D1的中点. 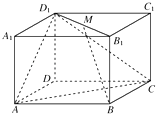
(1)求证:BM∥平面D1AC;
(2)求直线DD1与平面D1AC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数F(x)= ![]() t(t﹣4)dt在[﹣1,5]上( )
t(t﹣4)dt在[﹣1,5]上( )
A.有最大值0,无最小值
B.有最大值0,最小值 ![]()
C.有最小值 ![]() ,无最大值
,无最大值
D.既无最大值也无最小值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com