
【题目】如图所示,在三棱锥![]() 中,
中,![]() 是边长为4的正三角形,平面
是边长为4的正三角形,平面![]() 平面
平面![]() ,SA=SC=
,SA=SC=![]() ,M,N分别为AB,SB的中点.
,M,N分别为AB,SB的中点.
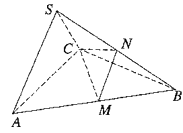
(1)求证:AC⊥SB;
(2)求二面角N-CM-B的余弦值;
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某超市在节日期间进行有奖促销,凡在该超市购物满![]() 元的顾客,将获得一次摸奖机会,规则如下:一个袋子装有
元的顾客,将获得一次摸奖机会,规则如下:一个袋子装有![]() 只形状和大小均相同的玻璃球,其中两只是红色,三只是绿色,顾客从袋子中一次摸出两只球,若两只球都是红色,则奖励
只形状和大小均相同的玻璃球,其中两只是红色,三只是绿色,顾客从袋子中一次摸出两只球,若两只球都是红色,则奖励![]() 元;共两只球都是绿色,则奖励
元;共两只球都是绿色,则奖励![]() 元;若两只球颜色不同,则不奖励.
元;若两只球颜色不同,则不奖励.
(1)求一名顾客在一次摸奖活动中获得![]() 元的概率;
元的概率;
(2)记![]() 为两名顾客参与该摸奖活动获得的奖励总数额,求随机变量
为两名顾客参与该摸奖活动获得的奖励总数额,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为提高玉米产量,某种植基地对单位面积播种数与每棵作物的产量之间的关系进行了研究,收集了![]() 块试验田的数据,得到下表:
块试验田的数据,得到下表:
试验田编号 |
|
|
|
|
|
|
|
|
|
|
|
(棵/) |
|
|
|
|
|
|
|
|
|
|
|
(斤/棵) |
|
|
|
|
|
|
|
|
|
|
|
技术人员选择模型![]() 作为
作为![]() 与
与![]() 的回归方程类型,令
的回归方程类型,令![]() ,
,![]() 相关统计量的值如下表:
相关统计量的值如下表:
|
|
|
|
|
|
|
|
由表中数据得到回归方程后进行残差分析,残差图如图所示:

(1)根据残差图发现一个可疑数据,请写出可疑数据的编号(给出判断即可,不必说明理由);
(2)剔除可疑数据后,由最小二乘法得到关于的线性回归方程![]() 中的
中的![]() ,求
,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)利用(2)得出的结果,计算当单位面积播种数![]() 为何值时,单位面积的总产量
为何值时,单位面积的总产量![]() 的预报值最大?(计算结果精确到
的预报值最大?(计算结果精确到![]() )
)
附:对于一组数据![]() ,
,![]() ,
,![]() ,
,![]() 其回归直线
其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为 ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(13分)设{an}是公比为正数的等比数列a1=2,a3=a2+4.
(Ⅰ)求{an}的通项公式;
(Ⅱ)设{bn}是首项为1,公差为2的等差数列,求数列{an+bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据市场调查,某种商品一年内每件出厂价在6千元的基础上,按月呈![]() 的模型波动(x为月份),已知3月份达到最高价8千元,7月份价格最低为4千元,该商品每件的售价为
的模型波动(x为月份),已知3月份达到最高价8千元,7月份价格最低为4千元,该商品每件的售价为![]() (x为月份),且满足
(x为月份),且满足![]() .
.
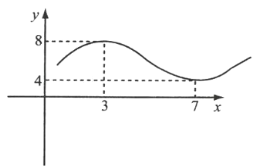
(1)分别写出该商品每件的出厂价函数![]() 和售价函数
和售价函数![]() 的解析式;
的解析式;
(2)问几月份的销售盈利最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com