
(本小题满分1 2分)
如图,四边形ABCD中,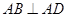 ,AD∥BC,AD =6,BC =4,AB =2,点E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABCD
,AD∥BC,AD =6,BC =4,AB =2,点E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABCD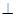 平面EFDC,设AD中点为P.
平面EFDC,设AD中点为P.
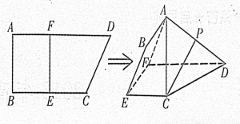
( I )当E为BC中点时,求证:CP//平面ABEF
(Ⅱ)设BE=x,问当x为何值时,三棱锥A-CDF的体积有最大值?并求出这个最大值。
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案科目:高中数学 来源:2011-2012学年福建省福州市高三第一学期期末质量检测文科数学 题型:解答题
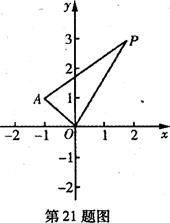
(本小题满分1 2分)在平面直角坐标系xOy中,已知点A(一1,1),P是动点,且三角形POA的三边所在直线的斜率满足kOP+kOA=kPA.
(I)求点P的轨迹C的方程;
(Ⅱ)若Q是轨迹C上异于点P的一个点,且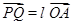 ,直线OP与QA交于点M,试探究:点M的横坐标是否为定值?并说明理由.
,直线OP与QA交于点M,试探究:点M的横坐标是否为定值?并说明理由.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省福州市高三第一学期期末质量检测文科数学 题型:解答题
.(本小题满分1 2分)设△ABC的内角A、B、C所对的边分别为a、b、c.已知a=3,B=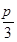 ,S△ABC=6
,S△ABC=6
( I )求△ABC的周长;
(Ⅱ)求sin2A的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com