
【题目】我们国家正处于老龄化社会中,老有所依也是政府的民生工程.某市共有户籍人口400万,其中老人(年龄60岁及以上)人数约有66万,为了解老人们的健康状况,政府从 老人中随机抽取600人并委托医疗机构免费为他们进行健康评估,健康状况共分为不能 自理、不健康尚能自理、基本健康、健康四个等级,并以80岁为界限分成两个群体进行 统计,样本分布被制作成如图表: 
(1)若采取分层抽样的方法再从样本中的不能自理的老人中抽取16人进一步了解他们的生活状况,则两个群体中各应抽取多少人?
(2)估算该市80岁及以上长者占全市户籍人口的百分比;
(3)据统计该市大约有五分之一的户籍老人无固定收入,政府计划为这部分老人每月发 放生活补贴,标准如下:①80岁及以上长者每人每月发放生活补贴200元;②80岁以下 老人每人每月发放生活补贴120元;③不能自理的老人每人每月额外发放生活补贴100 元.试估计政府执行此计划的年度预算.
【答案】
(1)解:数据整理如下表:
健康状况 | 健康 | 基本健康 | 不健康尚能自理 | 不能自理 |
80岁及以上 | 20 | 45 | 20 | 15 |
80岁以下 | 200 | 225 | 50 | 25 |
从图表中知不能自理的80岁及以上长者占比为: ![]() =
= ![]() ,
,
故抽取16人中不能自理的80岁及以上长者人数为16× ![]() =6.80岁以下长者人数为10人
=6.80岁以下长者人数为10人
(2)解:在600人中80岁及以上长者在老人中占比为: ![]() =
= ![]() ,
,
用样本估计总体,80岁及以上长者共有 ![]() 万,
万,
80岁及以上长者占户籍人口的百分比为 ![]() 100%=2.75%
100%=2.75%
(3)解:用样本估计总体,设任一户籍老人每月享受的生活补助为X元,
P(X=0)= ![]() ,P(X=120)=
,P(X=120)= ![]() ×
× ![]() =
= ![]() ,P(X=200)=
,P(X=200)= ![]() =
= ![]() ,
,
P(X=220)= ![]() =
= ![]() ,P(X=300)=
,P(X=300)= ![]() =
= ![]() ,
,
则随机变量X的分布列为:
X | 0 | 120 | 200 | 220 | 300 |
P |
|
|
|
|
|
EX=0× ![]() +120×
+120× ![]() +200×
+200× ![]() +220×
+220× ![]() +300×
+300× ![]() =28,
=28,
全市老人的总预算为28×12×66×104=2.2176×108元.
政府执行此计划的年度预算约为2.2176亿元
【解析】(1)数据整理如下表:
健康状况 | 健康 | 基本健康 | 不健康尚能自理 | 不能自理 |
80岁及以上 | 20 | 45 | 20 | 15 |
80岁以下 | 200 | 225 | 50 | 25 |
利用频率计算公式即可得出.(2)在600人中80岁及以上长者在老人中占比为: ![]() ,用样本估计总体,80岁及以上长者共有
,用样本估计总体,80岁及以上长者共有 ![]() 万,即可得出80岁及以上长者占户籍人口的百分比.(3)用样本估计总体,设任一户籍老人每月享受的生活补助为X元,P(X=0)=
万,即可得出80岁及以上长者占户籍人口的百分比.(3)用样本估计总体,设任一户籍老人每月享受的生活补助为X元,P(X=0)= ![]() ,P(X=120)=
,P(X=120)= ![]() ×
× ![]() ,P(X=200)=
,P(X=200)= ![]() ,P(X=220)=
,P(X=220)= ![]() ,P(X=300)=
,P(X=300)= ![]() ,及其数学期望.
,及其数学期望.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】在考试测评中,常用难度曲线图来检测题目的质量,一般来说,全卷得分高的学生,在某道题目上的答对率也应较高,如果是某次数学测试压轴题的第1、2问得分难度曲线图,第1、2问满分均为6分,图中横坐标为分数段,纵坐标为该分数段的全体考生在第1、2问的平均难度,则下列说法正确的是( ) 
A.此题没有考生得12分
B.此题第1问比第2问更能区分学生数学成绩的好与坏
C.分数在[40,50)的考生此大题的平均得分大约为4.8分
D.全体考生第1问的得分标准差小于第2问的得分标准差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式|x+3|﹣2x﹣1<0的解集为(x0 , +∞)
(Ⅰ)求x0的值;
(Ⅱ)若函数f(x)=|x﹣m|+|x+ ![]() |﹣x0(m>0)有零点,求实数m的值.
|﹣x0(m>0)有零点,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
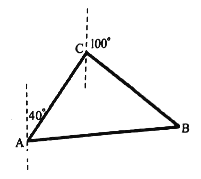
【题目】某渔船在航行中不幸遇险,发出呼叫信号,我海军舰艇在![]() 处获悉后,立即测出该渔船在方位角(从指北方向顺时针转到目标方向线的水平角)为
处获悉后,立即测出该渔船在方位角(从指北方向顺时针转到目标方向线的水平角)为![]() ,距离为15海里的
,距离为15海里的![]() 处,并测得渔船正沿方位角为
处,并测得渔船正沿方位角为![]() 的方向,以15海里/小时的速度向小岛
的方向,以15海里/小时的速度向小岛![]() 靠拢,我海军舰艇立即以
靠拢,我海军舰艇立即以![]() 海里/小时的速度前去营救,求舰艇靠近渔船所需的最少时间和舰艇的航向.
海里/小时的速度前去营救,求舰艇靠近渔船所需的最少时间和舰艇的航向.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构为了解某市民用电情况,抽查了该市100户居民月均用电量(单位:![]() ,以
,以![]() 分组的频率分布直方图如图所示.
分组的频率分布直方图如图所示.

(1)求样本中月均用电量为![]() 的用户数量;
的用户数量;
(2)估计月均用电量的中位数;
(3)在月均用电量为![]() 的四组用户中,用分层抽样的方法抽取22户居民,则月均用电量为
的四组用户中,用分层抽样的方法抽取22户居民,则月均用电量为![]() 的用户中应该抽取多少户?
的用户中应该抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过定点P(1,1),且倾斜角为 ![]() ,以坐标原点为极点,x轴的正半轴为极轴的坐标系中,曲线C的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴的坐标系中,曲线C的极坐标方程为 ![]() .
.
(1)求曲线C的直角坐标方程与直线l的参数方程;
(2)若直线l与曲线C相交于不同的两点A,B,求|AB|及|PA||PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某工厂开展群众体育活动的情况,拟采用分层抽样的方法从A,B,C三个区中抽取7个工厂进行调查,已知A,B,C区中分别有18,27,18个工厂
(Ⅰ)求从A,B,C区中分别抽取的工厂个数;
(Ⅱ)若从抽取的7个工厂中随机抽取2个进行调查结果的对比,求这2个工厂中至少有1个来自A区的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂对新研发的一种产品进行试销,得到如下数据表:
(1)根据上表求出回归直线方程 ![]() ,并预测当单价定为8.3元时的销量;
,并预测当单价定为8.3元时的销量;
(2)如果该工厂每件产品的成本为5.5元,利用所求的回归方程,要使得利润最大,单价应该定为多少?
附:线性回归方程 ![]() 中斜率和截距最小二乘估计计算公式:
中斜率和截距最小二乘估计计算公式: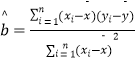 ,
, ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com