练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    t∈R，t∈(0，10)，由t确定两个任意点P(t，t)，Q(10－t，0)．问：①直线PQ是否能通过下面的点M(6，1)，N(4，5)；②在△OPQ内作内接正方形ABCD，顶点A、B在边OQ上，顶点C在边PQ上，顶点D在边OP上．

    (1)求证：顶点C一定在直线y＝x上．

    (2)求下图中阴影部分面积的最大值，并求这时顶点A、B、C、D的坐标．

    答案：
    解析：

    		 　　(1)略

    　　(1)略

    　　(2)A(，0)，B(5，0)，C(5，)，D(，)


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2004年高考教材全程总复习试卷·数学 题型：044

    设向量a＝(cos，cos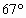)，b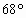＝(cos，cos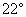)，c＝a＋tb(t∈R)

    (1)求a·b．

    (2)求|c|的最小值．

    查看答案和解析>>

    科目：高中数学 来源：浙江省杭州高中2006-2007学年度第一学期高三年级第三次月考　数学试题(理) 题型：038

    解答题：解答应写出文字说明，证明过程或演算步骤．

    设二次函数f(x)＝ax2＋bx＋c，(a，b，c∈R)满足下列条件：

    ①当x∈R时，f(x)的最小值为0，且f(x－1)＝f(－x－1)成立；

    ②当x∈(0，5)时，x≤f(x)≤2＋1恒成立．

    (1)

    求f(1)的值

    (2)

    求f(x)的解析式

    (3)

    求最大的实数m(m＞1)，使得存在实数t，只要当x∈时，就有f(x＋t)≤x成立．

    查看答案和解析>>

    科目：高中数学 来源：浙江省杭州地区七校2006－2007学年度第一学期高三数学文科11月联考试卷 题型：044

    解答题：解答应写出文字说明．证明过程或演算步骤＋

    已知定义域为R的单调函数f(x)满足f(x＋y)＝f(x)＋f(y)，且f(1)＝2，

    (1)

    判断f(x)的奇偶性和单调性

    (2)

    解不等式

    (3)

    若f(klog2t)＋f(log2t－log22t－2)＜0对t∈(0,＋∞)恒成立，求实数k的取值范围.

    查看答案和解析>>

    科目：高中数学 来源：重庆南开中学2007级高三年级11月份月考、数学(理)试题 题型：044

    解答题：解答应写出文字说明、证明过程或演算步骤．

    已知α，β是方程4x2－4tx－1＝0(t∈R)的两个不等实根，函数的定义域为[α，β]

    (1)

    证明f(x)在区间[α，β]上是增函数

    (2)

    对任意x1，x2∈[α，β]，K≥|f(x1)－f(x2)|恒成立，求K的最小值g(t)

    (3)

    若对锐角u1，u2有，试证：

    查看答案和解析>>

    同步练习册答案