
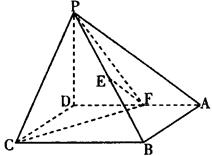

 ,
,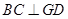 从而证明出
从而证明出 平面
平面 ,然后证明出GD//EF,问题到此基本得以解决.
,然后证明出GD//EF,问题到此基本得以解决. ,易证:
,易证:

 ,
,

 ,所以
,所以 是二面角
是二面角 的平面角,然后解三角形求角即可
的平面角,然后解三角形求角即可 的中点
的中点 ,连结
,连结 ,
,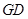 则
则 //
// ,且
,且 ,
,
 //
// ,且
,且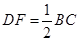 ,∴
,∴ //
// 且
且 ,∴四边形
,∴四边形 为平行四边形,∴
为平行四边形,∴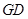 //
// .……………………… 3分
.……………………… 3分 平面
平面 ,∴
,∴ ,又
,又 ,∴
,∴ 平面
平面 ,又
,又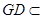 平面
平面 ,∴
,∴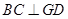 ,在等腰直角三角形
,在等腰直角三角形 中,由
中,由 为
为 中点,∴
中点,∴ ,
, ,∴
,∴ 平面
平面 , ……………………………………………… 5分
, ……………………………………………… 5分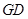 //
// ,∴
,∴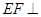 平面
平面 . ………………………………………………… 6分
. ………………………………………………… 6分 ,∵
,∵ ,
, //
// ,∴
,∴

 , ∵
, ∵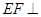 平面
平面 ,∴
,∴ ,
, ,∴
,∴ 平面
平面 ,
,


 , ∴
, ∴ 是二面角
是二面角 的平面角.…………… 9分
的平面角.…………… 9分 中,
中,
 ,
, ,
, ,所以二面角
,所以二面角 的平面角的余弦值为
的平面角的余弦值为


科目:高中数学 来源:不详 题型:解答题
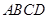 和矩形
和矩形 所在的平面互相垂直,
所在的平面互相垂直,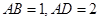 ,
,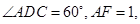
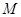 是线段
是线段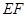 的中点.
的中点.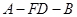 的正弦值;
的正弦值;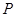 为一动点,若点
为一动点,若点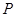 从
从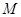 出发,沿棱按照
出发,沿棱按照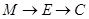 的路线运动到点
的路线运动到点 ,求这一过程中形成的三棱锥
,求这一过程中形成的三棱锥 的体积的最小值.
的体积的最小值.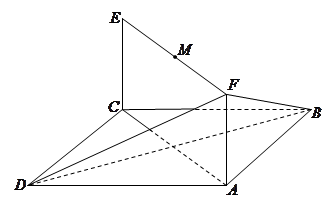
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com