Question

已知直线l经过点A(2,4)，且被平行直线l₁：x－y＋1＝0与l₂：x－y－1＝0所截得的线段的中点M在直线x＋y－3＝0上．求直线l的方程．

Answer 1

[解析]　解法一：∵点M在直线x＋y－3＝0上，

∴设点M坐标为(t,3－t)，则点M到l₁、l₂的距离相等，

即＝，

解得t＝，∴M.

又l过点A(2,4)，

由两点式得＝，

即5x－y－6＝0，

故直线l的方程为5x－y－6＝0.

解法二：设与l₁、l₂平行且距离相等的直线l₃：x－y＋c＝0，由两平行直线间的距离公式得＝，解得c＝0，即l₃：x－y＝0.由题意得中点M在l₃上，又点M在x＋y－3＝0上．

解方程组，得.

∴M.又l过点A(2,4)，

故由两点式得直线l的方程为5x－y－6＝0.

解法三：由题意知直线l的斜率必存在，

设l：y－4＝k(x－2)，

由，得.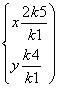

∴直线l与l₁、l₂的交点分别为，

.

∵M为中点，∴M.

又点M在直线x＋y－3＝0上，

∴＋－3＝0，解得k＝5.

故所求直线l的方程为y－4＝5(x－2)，

即5x－y－6＝0.