
【题目】已知函数![]() (
(![]() 且
且![]() ),
),
(1)讨论![]() 的奇偶性与单调性;
的奇偶性与单调性;
(2)求![]() 的反函数
的反函数![]() ;
;
(3)若![]() ,解关于x的不等式
,解关于x的不等式![]() .
.
【答案】(1)奇函数,当![]() 时,单调递增,当
时,单调递增,当![]() 时,单调递减;(2)
时,单调递减;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)根据函数奇偶性的定义可判断出函数![]() 的奇偶性;再根据函数单调性的定义并对底数
的奇偶性;再根据函数单调性的定义并对底数![]() 分类讨论,可判断出
分类讨论,可判断出![]() 在
在![]() 上的单调性;
上的单调性;
(2)根据反函数的求法直接求解即可;
(3)根据![]() 可求出
可求出![]() 的值,进而可求出
的值,进而可求出![]() 的值域,然后对
的值域,然后对![]() 分类讨论即可求出不等式的解集.
分类讨论即可求出不等式的解集.
(1)由![]() ,解得
,解得![]() ,所以函数
,所以函数![]() 的定义域为
的定义域为![]() ,关于原点对称.
,关于原点对称.
因为![]() ,
,
所以函数![]() 是奇函数.
是奇函数.
对任意的![]() ,且
,且![]() ,则
,则
![]() ,
,
因为![]() ,
,
所以![]() ,所以
,所以![]() ,
,
①当![]() 时,
时,![]() ,所以
,所以![]() ,即
,即![]() ,
,
此时函数![]() 是
是![]() 上的单调减函数;
上的单调减函数;
②当![]() 时,
时,![]() ,所以所以
,所以所以![]() ,即
,即![]() ,
,
此时函数![]() 是
是![]() 上的单调增函数.
上的单调增函数.
(2)令![]() ,
,
所以![]() ,
,
所以![]() ,所以
,所以![]() .
.
(3)因为![]() ,即
,即![]() ,解得
,解得![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以当![]() 时,不等式的解集为
时,不等式的解集为![]() ;
;
当![]() 时,不等式的解集为
时,不等式的解集为![]() ;
;
当![]() 时,不等式的解集为
时,不等式的解集为![]() .
.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设![]() 为曲线
为曲线![]() 上的点,
上的点,![]() ,垂足为
,垂足为![]() ,若
,若![]() 的最小值为
的最小值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国是茶的故乡,也是茶文化的发源地.中国茶的发现和利用已有四千七百多年的历史,且长盛不衰,传遍全球.为了弘扬中国茶文化,某酒店推出特色茶食品“金萱排骨茶”,为了解每壶“金萱排骨茶”中所放茶叶量![]() 克与食客的满意率
克与食客的满意率![]() 的关系,通过试验调查研究,发现可选择函数模型
的关系,通过试验调查研究,发现可选择函数模型![]() 来拟合
来拟合![]() 与
与![]() 的关系,根据以下数据:
的关系,根据以下数据:
茶叶量 | 1 | 2 | 3 | 4 | 5 |
| 4.34 | 4.36 | 4.44 | 4.45 | 4.51 |
可求得y关于x的回归方程为( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() )上的两个动点
)上的两个动点![]() 和
和![]() ,焦点为F.线段AB的中点为
,焦点为F.线段AB的中点为![]() ,且A,B两点到抛物线的焦点F的距离之和为8.
,且A,B两点到抛物线的焦点F的距离之和为8.
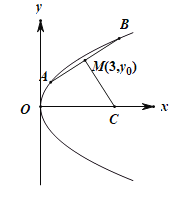
(1)求抛物线的标准方程;
(2)若线段AB的垂直平分线与x轴交于点C,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两袋装有大小相同的红球和白球,甲袋装有2个红球和2个白球,乙袋装有2个红球和n个白球.现从甲、乙两袋中各任取2个球.
(1)若![]() ,求取到的4个球全是红球的概率;
,求取到的4个球全是红球的概率;
(2)若取到的4个球中至少有2个红球的概率为![]() ,求n.
,求n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某校新、老校区之间开车单程所需时间为T,T只与道路畅通状况有关,对其容量为100的样本进行统计,结果如下:
T(分钟) | 25 | 30 | 35 | 40 |
频数(次) | 20 | 30 | 40 | 10 |
刘教授驾车从老校区出发,前往新校区做一个50分钟的讲座,结束后立即返回老校区,求刘教授从离开老校区到返月老校区共用时间不超过120分钟的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个透明密闭的立方体容器,恰好盛有该容器一半容积的水任意转动这一立方体,则水面在容器中的形状可能是________.(从正方形,三角形,菱形,矩形,等腰梯形,正六边形,正五边形中选取正确的都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com