
【题目】如图,l1,l2是通过某城市开发区中心O的两条南北和东西走向的街道,连结M、N两地之间的铁路线是圆心在l2上的一段圆弧.若点M在点O正北方向,且|MO|=3 km,点N到l1,l2的距离分别为4 km和5 km.

(1)建立适当的坐标系,求铁路线所在圆弧的方程;
(2)若该城市的某中学拟在点O正东方向选址建分校,考虑环境问题,要求校址到点O的距离大于4 km,并且铁路线上任意一点到校址的距离不能少于![]() km,求该校址距点O的最近距离.(注:校址视为一个点)
km,求该校址距点O的最近距离.(注:校址视为一个点)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某种产品的广告费支出![]() (百万元)与销售额
(百万元)与销售额![]() (百万元)之间有如下对应数据:
(百万元)之间有如下对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 50 | 60 | 70 |
如果![]() 与
与![]() 之间具有线性相关关系.
之间具有线性相关关系.
(1)作出这些数据的散点图;
(2)求这些数据的线性回归方程![]() ;
;
(3)预测当广告费支出为9百万元时的销售额。 ( 参考数据: ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设某种设备使用的年限x(年)与所支出的维修费用y(万元)有以下统计资料:
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2 | 4 | 5 | 6 | 7 |
若由资料知y对x呈线性相关关系。试求:
(1)求![]() ; (2)线性回归方程
; (2)线性回归方程![]() ;
;
(3)估计使用10年时,维修费用是多少?
附:利用“最小二乘法”计算a,b的值时,可根据以下公式:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点M是棱长为2的正方体的棱AD的中点,P是平面![]() 内一点,若面
内一点,若面![]() 分别与面ABCD和面
分别与面ABCD和面![]() 所成的锐二面角相等,则
所成的锐二面角相等,则![]() 长度的最小值是( )
长度的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn=3n﹣1.
(1)求a1 , a2 , a3的值;
(2)求数列{an}的通项公式;
(3)求数列{nan}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和记为Sn , a1=1,an+1=2Sn+1(n≥1).
(1)求{an}的通项公式;
(2)等差数列{bn}的各项为正,其前n项和为Tn , 且T3=15,又a1+b1 , a2+b2 , a3+b3成等比数列,求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
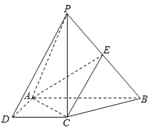
【题目】如图,在四棱锥![]() 中,
中, ![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点.
的中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 的余弦值为
的余弦值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com