

分析 利用旋转的性质得出∠AOH=∠AHO,进而得出OA=AH=AE+FC=AE+GC,进而求出OB=BK=BG+FD=BG+ED,即可得出答案.
解答  解:设E、F、G为三边的切点,将△OFC绕O点旋转到△OEH,H在射线ED上,
解:设E、F、G为三边的切点,将△OFC绕O点旋转到△OEH,H在射线ED上,
设θ=∠OCF=∠OHE=∠OCG,
∵四边形ABCD内接于圆,
∴∠A=180°-2θ,∠AOH=180°-(θ+180°-2θ)=θ=∠AHO,
因此,OA=AH=AE+FC=AE+GC…①
用同样的方法,即将△OFD绕O点顺时针旋转到△OGK,K在GC上,
得到OB=BK=BG+FD=BG+ED…②,
①+②得AB=AD+BC.
点评 此题主要考查了旋转的性质,通过旋转将问题“化整为零”,然后再“各个击破”是解题关键.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | $[{1,\frac{1}{2}+ln2}]$ | C. | (-∞,e-1] | D. | [1,e-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
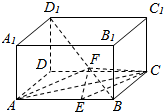 如图,在长方体ABCD-A1B1C1D1中,AB=3,AA1=AD=2,BE=1,F是BD1上一点,且EF∥平面ADD1A1,则三棱锥E-AFC的体积为$\frac{4}{9}$.
如图,在长方体ABCD-A1B1C1D1中,AB=3,AA1=AD=2,BE=1,F是BD1上一点,且EF∥平面ADD1A1,则三棱锥E-AFC的体积为$\frac{4}{9}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
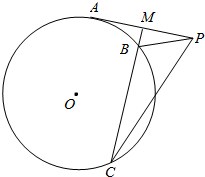 自⊙O外一点p引切线与⊙O切于点A,M为PA的中点,过M引割线交⊙O于B、C两点.
自⊙O外一点p引切线与⊙O切于点A,M为PA的中点,过M引割线交⊙O于B、C两点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
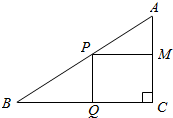 直角三角形ABC的直角顶点为C,且AC=3cm,BC=4cm,P为斜边AB上一点,PQ平行于AC且交BC于点Q,PM平行于BC且交AC于点M,问点P在边AB何处时,矩形PQCM的面积最大?最大面积是多少?
直角三角形ABC的直角顶点为C,且AC=3cm,BC=4cm,P为斜边AB上一点,PQ平行于AC且交BC于点Q,PM平行于BC且交AC于点M,问点P在边AB何处时,矩形PQCM的面积最大?最大面积是多少?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com