
���� ��1����ABΪx�ᡢ��AB���д���ֱ������ϵ�����ı��εĶ���C�������ǣ�x��y�����������|CA|+|CB|=4��|AB|=2����켣Ϊ��Բ�������������Բ���̣�
��2����ͼ�������ε������ʽ����۹������S=2S��ABC=2|yC|��������Բ�ķ�Χ����۹�����������
��3����ʵ������ת��Ϊ��ֱ��l����Բ�ཻ���ҳ����⣬��P��x1��y1����Q��x2��y2����������ֱ�߷��̺���Բ������ȥy���ɸ���ϵ���Ĺ�ϵ���Լ��ҳ���ʽ������⣮
��� �⣺��1����ABΪx�ᣬ��AB���д���ֱ������ϵ��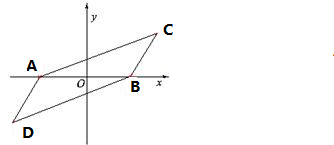 ����ͼ��
����ͼ��
���ı��εĶ���C�������ǣ�x��y������D��-x��-y����A��-1��0����B��1��0����
������ã�|CA|+|CB|=4��|AB|=2��
���Ե�C�켣Ϊ��Բ����a=2��c=1��b=$\sqrt{3}$��
�ı�������������Ĺ켣������$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$��
��2����ͼ�ã��۹���������S=2S��ABC=2��$\frac{1}{2}$|AB||yC|=2|yC|��
��Ϊ|yC|��$\sqrt{3}$����2|yC|��2$\sqrt{3}$��
����ũ�����������ܴﵽ2$\sqrt{3}$km2��
��3����Ϊֱ���Ͳ���С���պ�ͨ����A����l��AB��45��ǣ�����ֱ��l�ķ���Ϊ��y=x+1��
��ֱ��l����Բ$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$�ཻ�ڵ�P��Q���㣬����С�����ܱ��۹�Χס�IJ���ΪPQ��
��P��x1��y1����Q��x2��y2����
��ֱ������Բ�����ã�7x2+8x-8=0��
����x1+x2=-$\frac{8}{7}$��x1x2=-$\frac{8}{7}$��
��|PQ|=$\sqrt{2}•\sqrt{\frac{64}{49}-4����-\frac{8}{7}��}$=$\frac{24}{7}$��km����
�����ݲ����IJ���Ϊ$\frac{24}{7}$km��
���� ���⿼��Բ������ʵ�������е�Ӧ�ã��漰��Բ�Ķ��塢�����̺����ʣ�ֱ����Բ��λ�ù�ϵ���ҳ���ʽ��Τ�ﶨ����Ӧ�ã�����ʱҪ�������⡢��ϸ�����Ŀ��ӱ��������ѧ��ʵ������Ĺ�ϵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $-\frac{1}{2}$ | B�� | $-\frac{3}{2}$ | C�� | $-\frac{{\sqrt{3}}}{2}-1$ | D�� | $\frac{{\sqrt{3}}}{2}-1$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{4}$ | B�� | $\frac{3��}{8}$ | C�� | $\frac{3��}{4}$ | D�� | $\frac{5��}{8}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com