
(本题12分)为了研究化肥对小麦产量的影响,某科学家将一片土地划分成200个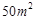 的小块,并在100个小块上施用新化肥,留下100个条件大体相当的小块不施用新化肥.下表1和表2分别是施用新化肥和不施用新化肥的小麦产量频数分布表(小麦产量单位:kg)
的小块,并在100个小块上施用新化肥,留下100个条件大体相当的小块不施用新化肥.下表1和表2分别是施用新化肥和不施用新化肥的小麦产量频数分布表(小麦产量单位:kg)
表1:施用新化肥小麦产量频数分布表
| 小麦产量 | 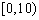 | 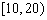 | 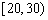 | 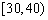 | 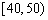 |
| 频数 | 10 | 35 | 40 | 10 | 5 |
| 小麦产量 | 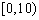 | 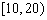 | 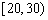 | 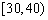 |
| 频数 | 15 | 50 | 30 | 5 |
| | 小麦产量小于20kg | 小麦产量不小于20kg | 合计 |
| 施用新化肥 |  | 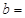 | |
| 不施用新化肥 | 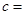 |  | |
| 合计 | | | 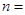 |
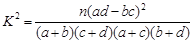
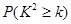 | 0.050 | 0.010 | 0.005 | 0.001 |
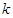 | 3.841 | 6.635 | 7.879 | 10.828 |
(1)见解析; (2) 施用化肥的平均产量为21.5,不施用新化肥的平均产量为17.5; (3)列量表见解析,99.5%。
解析试题分析: 4分
4分
(2)施用化肥的一小块土地小麦平均产量为
5×0.1+15×0.35+25×0.4+35×0.1+45×0.05=21.5 ………6分
不施用新化肥的一小块土地小麦平均产量为
5×0.15+15×0.5+25×0.3+35×0.05=17.5 ………8分
(3)表3 小麦产量小于20kg 小麦产量不小于20kg 合计 施用新化肥 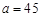

100 不施用新化肥 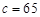
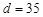
100 合计 110 90 
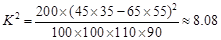 ………11分
………11分
由于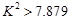 ,所以有99.5%的把握认为施用新化肥和不施用新化肥的小麦产量有差异 ………12分
,所以有99.5%的把握认为施用新化肥和不施用新化肥的小麦产量有差异 ………12分
考点:频率分布直方图;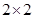 列联表;独立性检验。
列联表;独立性检验。
点评:在频率分布直方图中:小长方形的面积=组距× =频率,各个长方形的面积之和等于1。属于基础题。
=频率,各个长方形的面积之和等于1。属于基础题。


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
调查某桑场采桑员和辅助工桑毛虫皮炎发病情况结果如下表:利用2×2列联表的独立性检验估计“患桑毛虫皮炎病与采桑”是否有关?认为两者有关系会犯错误的概率是多少?
| | 采桑 | 不采桑 | 合计 |
| 患者人数 | 18 | 12 | |
| 健康人数 | 5 | 78 | |
| 合计 | | | |
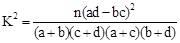
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是: .
.
(1)求图中x的值;
(2)从成绩不低于80分的学生中按分层抽样抽取4人,选其中2人为数学课代表,求这两个人的数学成绩不在同一分数段的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某高校在2013年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组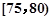 ,第2组
,第2组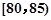 ,第3组
,第3组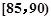 ,第4组
,第4组 ,第5组
,第5组 ,得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.
,得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.
(1)求出第4组的频率;
(2)如果用分层抽样的方法从“优秀”和“良好” 的学生中选出5人,再从这5人中选2人,那么至少有一人是“优秀”的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题12分)一个质地均匀的正四面体的四个面上分别标示着数字1、2、3、4,一个质地均匀的骰子(正方体)的六个面上分别标示数字1、2、3、4、5、6,先后抛掷一次正四面体和骰子。
⑴列举出全部基本事件;
⑵求被压在底部的两个数字之和小于5的概率;
⑶求正四面体上被压住的数字不小于骰子上被压住的数字的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
第8届中学生模拟联合国大会将在本校举行,为了搞好接待工作,组委会招募了12名男志愿者和18名女志愿者.将这30名志愿者的身高编成如下茎叶图(单位:cm):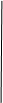
 男 女
男 女 15 7 7 8 9 9 9
15 7 7 8 9 9 9
9 8 16 0 0 1 2 4 5 8 9
8 6 5 0 17 2 5 6
7 4 2 1 18 0
1 0 19
若男生身高在180cm以上(包括180cm)定义为“高个子”, 在180cm以下(不包括180cm)定义为“非高个子”, 女生身高在170cm以上(包括170cm)定义为“高个子”,在170cm以下(不包括170cm)定义为“非高个子”.
(1)如果用分层抽样的方法从“高个子”和“非高个子”中抽取6人,则应分别抽取“高个子”、“非高个子”各几人?
(2)从(1)中抽出的6人中选2人担任领座员,那么至少有一人是“高个子”的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分)惠州市在每年的春节后,市政府都会发动公务员参与到植树活动中去.林管部门在植树前,为保证树苗的质量,都会在植树前对树苗进行检测.现从甲乙两种树苗中各抽测了10株树苗的高度,量出的高度如下(单位:厘米)
甲:37,21,31,20,29,19,32,23,25,33
乙:10,30,47,27,46,14,26,10,44,46
(1)根据抽测结果,完成答题卷中的茎叶图,并根据你填写的茎叶图,对甲、乙两种树苗的高度作比较,写出两个统计结论;
(2)设抽测的10株甲种树苗高度平均值为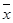 ,将这10株树苗的高度依次输入如图程序框图进行运算,问输出的S大小为多少?并说明S的统计学意义.
,将这10株树苗的高度依次输入如图程序框图进行运算,问输出的S大小为多少?并说明S的统计学意义.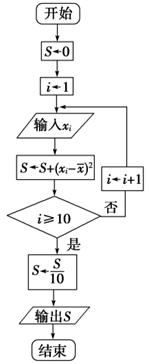
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如下表.
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
三、解答题:解答应写出文字说明、证明过程或演算步骤(本大题共6个大题,共76分)。
17.(12分)以下资料是一位销售经理收集来的每年销售额和销售经验年数的关系:
| 销售经验(年) | 1 | 3 | 4 | 4 | 6 | 8 | 10 | 10 | 11 | 13 |
| 年销售额(千元) | 80 | 97 | 92 | 102 | 103 | 111 | 119 | 123 | 117 | 136 |
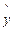 =78+4.2x,计算
=78+4.2x,计算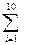 (yi-
(yi-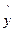 i)2;
i)2; 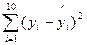 ;
;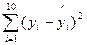 的大小.
的大小.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com