
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() .
.
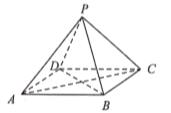
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)通过菱形的性质证得![]() ,通过等腰三角形的性质证得
,通过等腰三角形的性质证得![]() ,由此证得
,由此证得![]() 平面
平面![]() ,从而证得平面
,从而证得平面![]() 平面
平面![]() .
.
(2)方法一通过几何法作出二面角![]() 的平面角,解三角形求得二面角的余弦值.方法而通过建立空间直角坐标系,利用平面
的平面角,解三角形求得二面角的余弦值.方法而通过建立空间直角坐标系,利用平面![]() 和平面
和平面![]() 的法向量,计算出二面角的余弦值.
的法向量,计算出二面角的余弦值.
(1)证明:记![]() ,连接
,连接![]() .
.
因为底面![]() 是菱形,
是菱形,
所以![]() ,
,![]() 是
是![]() 的中点.
的中点.
因为![]() ,所以
,所以![]() .
.
因为![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)因为底面![]() 是菱形,
是菱形,![]() ,
,![]() ,
,
所以![]() 是等边三角形,即
是等边三角形,即![]() .
.
因为![]() ,所以
,所以![]() .
.
又![]() ,
,![]() ,所以
,所以![]() ,
,
即![]() .
.
方法一:因为![]() 是
是![]() 的中点,所以
的中点,所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() 和
和![]() 都是等腰三角形.
都是等腰三角形.
取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() ,且
,且![]() ,
,
所以![]() 是二面角
是二面角![]() 的平面角.
的平面角.
因为![]() ,且
,且![]() ,
,
所以![]() .
.
因为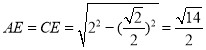 ,
,
![]() ,
,
所以![]() .
.
所以二面角![]() 的余弦值为
的余弦值为![]() .
.
方法二:如图,以![]() 为坐标原点,
为坐标原点,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]()
由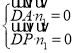 ,得
,得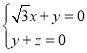 ,
,
令![]() ,得
,得![]() .
.
同理,可求平面![]() 的法向量
的法向量![]() .
.
所以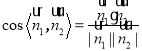

![]() .
.
所以,二面角![]() 的余弦值为
的余弦值为![]() .
.



科目:高中数学 来源: 题型:
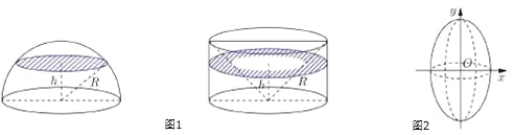
【题目】(数学文卷·2017届重庆十一中高三12月月考第16题) 现介绍祖暅原理求球体体积公式的做法:可构造一个底面半径和高都与球半径相等的圆柱,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥,用这样一个几何体与半球应用祖暅原理(图1),即可求得球的体积公式.请研究和理解球的体积公式求法的基础上,解答以下问题:已知椭圆的标准方程为![]() ,将此椭圆绕y轴旋转一周后,得一橄榄状的几何体(图2),其体积等于______.
,将此椭圆绕y轴旋转一周后,得一橄榄状的几何体(图2),其体积等于______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】军训时,甲、乙两名同学进行射击比赛,共比赛10场,每场比赛各射击四次,且用每场击中环数之和作为该场比赛的成绩.数学老师将甲、乙两名同学的10场比赛成绩绘成如图所示的茎叶图,并给出下列4个结论:(1)甲的平均成绩比乙的平均成绩高;(2)甲的成绩的极差是29;(3)乙的成绩的众数是21;(4)乙的成绩的中位数是18.则这4个结论中,正确结论的个数为( )

A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着西部大开发的深入,西南地区的大学越来越受到广大考生的青睐,下表是西南地区某大学近五年的录取平均分高于省一本线分值对比表:
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
录取平均分高于省一本线分值 | 28 | 34 | 41 | 47 | 50 |
(1)根据上表数据可知,![]() 与
与![]() 之间存在线性相关关系,求
之间存在线性相关关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)假设2020年该省一本线为520分,利用(1)中求出的回归方程预测2020年该大学录取平均分.
参考公式: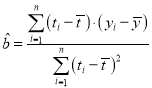 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从10种不同的作物种子中选出6种分别放入6个不同的瓶子中,每瓶不空,如果甲、乙两种种子都不许放入第一号瓶子内,那么不同的放法共有( )
A.![]() 种B.
种B.![]() 种C.
种C.![]() 种D.
种D.![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() 内一点
内一点![]() ,
,![]() 点为圆
点为圆![]() 上任意一点,线段
上任意一点,线段![]() 的垂直平分线与线段
的垂直平分线与线段![]() 连线交于点
连线交于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点
,过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,求
,求![]() 的内切圆半径的最大值.
的内切圆半径的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂有甲,乙两个车间生产同一种产品,,甲车间有工人![]() 人,乙车间有工人
人,乙车间有工人![]() 人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,甲车间抽取的工人记作第一组,乙车间抽取的工人记作第二组,并对他们中每位工人生产完成的一件产品的事件(单位:
人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,甲车间抽取的工人记作第一组,乙车间抽取的工人记作第二组,并对他们中每位工人生产完成的一件产品的事件(单位:![]() )进行统计,按照
)进行统计,按照![]() 进行分组,得到下列统计图.
进行分组,得到下列统计图.

![]() 分别估算两个车间工人中,生产一件产品时间少于
分别估算两个车间工人中,生产一件产品时间少于![]() 的人数
的人数
![]() 分别估计两个车间工人生产一件产品时间的平均值,并推测车哪个车间工人的生产效率更高?
分别估计两个车间工人生产一件产品时间的平均值,并推测车哪个车间工人的生产效率更高?
![]() 从第一组生产时间少于
从第一组生产时间少于![]() 的工人中随机抽取
的工人中随机抽取![]() 人,记抽取的生产时间少于
人,记抽取的生产时间少于![]() 的工人人数为随机变量
的工人人数为随机变量![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com