
【题目】函数![]() .
.
(1)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,
时,![]() 时,
时,![]() 恒成立,求正整数
恒成立,求正整数![]() 的最大值.
的最大值.
【答案】(1)见解析
(2)![]()
【解析】
(1)对![]() 求导,再因式分解,讨论每个因式的正负,再判断
求导,再因式分解,讨论每个因式的正负,再判断![]() 的正负,进而判断
的正负,进而判断![]() 的单调性;(2)代入
的单调性;(2)代入![]() ,将不等式
,将不等式![]() 中的
中的![]() 和
和![]() 分离在不等号两边,然后讨论不等号含有
分离在不等号两边,然后讨论不等号含有![]() 一边的函数的单调性,进而判断最值,再计算
一边的函数的单调性,进而判断最值,再计算![]() 的取值范围,由
的取值范围,由![]() 是正整数的条件可求出
是正整数的条件可求出![]() 的最大值.
的最大值.
解:(1)函数![]() 的定义域为
的定义域为![]() ,
,![]()
①当![]() 时,因为
时,因为![]() ,故有
,故有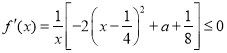 .
.
此时函数![]() 在区间
在区间![]() 单调递减.
单调递减.
②当![]() ,有
,有![]() ,方程
,方程![]() 的两根分别是:
的两根分别是:
![]()
![]() 函数
函数![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 函数
函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 函数
函数![]() 在
在![]() 上单调递减.
上单调递减.
③当![]() 时,易知
时,易知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
综上所述,当![]() 时,
时,![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 单调递减.
单调递减.
(2)当![]()
设![]()
![]() 当
当![]() 时,有
时,有![]() ,
,
设![]()
![]() 在
在![]() 上单调递增,
上单调递增,
又![]() 在
在![]() 上的函数图像是一条不间断的曲线,
上的函数图像是一条不间断的曲线,
且![]() ,
,![]()
存在唯一的![]() ,使得
,使得![]() ,即
,即![]() .
.
当![]() ;
;
当![]() ,
,
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]()
![]() 在
在![]() 上单调递减,
上单调递减,
![]() ,
,![]()
![]() 时,不等式
时,不等式![]() 对任意
对任意![]() 恒成立,
恒成立,
![]() 正整数
正整数![]() 的最大值是3.
的最大值是3.


科目:高中数学 来源: 题型:
【题目】(本小题满分12分,(1)小问7分,(2)小问5分)
设函数![]()
(1)若![]() 在
在![]() 处取得极值,确定
处取得极值,确定![]() 的值,并求此时曲线
的值,并求此时曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若![]() 在
在![]() 上为减函数,求
上为减函数,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们正处于一个大数据飞速发展的时代,对于大数据人才的需求也越来越大,其岗位大致可分为四类:数据开发、数据分析、数据挖掘、数据产品.某市2019年这几类工作岗位的薪资(单位:万元/月)情况如下表所示:
薪资
岗位 |
|
|
|
|
数据开发 |
|
|
|
|
数据分析 |
|
|
|
|
数据挖掘 |
|
|
|
|
数据产品 |
|
|
|
|
由表中数据可得该市各类岗位的薪资水平高低情况为( )
A.数据挖掘>数据开发>数据产品>数据分析
B.数据挖掘>数据产品>数据开发>数据分析
C.数据挖掘>数据开发>数据分析>数据产品
D.数据挖掘>数据产品>数据分析>数据开发
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科研小组为了研究一种治疗新冠肺炎患者的新药的效果,选50名患者服药一段时间后,记录了这些患者的生理指标![]() 和
和![]() 的数据,并统计得到如下的
的数据,并统计得到如下的![]() 列联表(不完整):
列联表(不完整):
|
| 合计 | |
| 12 | 36 | |
| 7 | ||
合计 |
其中在生理指标![]() 的人中,设
的人中,设![]() 组为生理指标
组为生理指标![]() 的人,
的人,![]() 组为生理指标
组为生理指标![]() 的人,他们服用这种药物后的康复时间(单位:天)记录如下:
的人,他们服用这种药物后的康复时间(单位:天)记录如下:
![]() 组:10,11,12,13,14,15,16
组:10,11,12,13,14,15,16
![]() 组:12,13,15,16,17,14,25
组:12,13,15,16,17,14,25
(Ⅰ)填写上表,并判断是否有95%的把握认为患者的两项生理指标![]() 和
和![]() 有关系;
有关系;
(Ⅱ)从![]() ,
,![]() 两组随机各选1人,
两组随机各选1人,![]() 组选出的人记为甲,
组选出的人记为甲,![]() 组选出的人记为乙,求甲的康复时间比乙的康复时间长的概率.
组选出的人记为乙,求甲的康复时间比乙的康复时间长的概率.
附: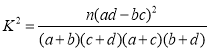 ,其中
,其中![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“垛积术”是我国古代数学的重要成就之一.南宋数学家杨辉在《详解九章算法》中记载了“方垛”的计算方法:“果子以垛,下方十四个,问计几何?术曰:下方加一,乘下方为平积.又加半为高,以乘下方为高积.如三而一.”意思是说,将果子以方垛的形式摆放(方垛即每层均为正方形,自下而上每层每边果子数依次递减1个,最上层为1个),最下层每边果子数为14个,问共有多少个果子?计算方法用算式表示为![]() .利用“方垛”的计算方法,可计算最下层每边果子数为14个的“三角垛”(三角垛即每层均为正三角形,自下而上每层每边果子数依次递减1个,最上层为1个)共有果子数为( )
.利用“方垛”的计算方法,可计算最下层每边果子数为14个的“三角垛”(三角垛即每层均为正三角形,自下而上每层每边果子数依次递减1个,最上层为1个)共有果子数为( )
A.420个B.560个C.680个D.1015个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,AB是圆O:x2+y2=1的直径,且点A在第一象限;圆O1:(x﹣a)2+y2=r2(a>0)与圆O外离,线段AO1与圆O1交于点M,线段BM与圆O交于点N,且![]() ,则a的取值范围为_______.
,则a的取值范围为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于圆周率,数学发展史上出现过许多很有创意的求法,如著名的浦丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计π的值:先请120名同学每人随机写下一个都小于1的正实数对(x,y)且x+y>1;再统计两数能与1构成钝角三角形三边的数对(x,y)的个数m,最后再根据统计数m估计π的值,假如统计结果是m=72,那么可以估计π的值约为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为支援武汉的防疫,某医院职工踊跃报名,其中报名的医生18人,护士12人,医技6人,根据需要,从中抽取一个容量为n的样本参加救援队,若采用系统抽样和分层抽样,均不用剔除人员.当抽取n+1人时,若采用系统抽样,则需剔除1个报名人员,则抽取的救援人员为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com