
【题目】![]() 三个班共有
三个班共有![]() 名学生,为调查他们的上网情况,通过分层抽样获得了部分学生一周的上网时长,数据如下表(单位:小时):
名学生,为调查他们的上网情况,通过分层抽样获得了部分学生一周的上网时长,数据如下表(单位:小时):
|
|
|
|
|
|
(1)试估计![]() 班的学生人数;
班的学生人数;
(2)从这120名学生中任选1名学生,估计这名学生一周上网时长超过15小时的概率;
(3)从A班抽出的6名学生中随机选取2人,从B班抽出的7名学生中随机选取1人,求这3人中恰有2人一周上网时长超过15小时的概率.
【答案】(1)36;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)利用分层抽样的方法即可得到答案;
(2)利用古典概率的公式即可得到答案;
(3)利用分类和分步计数原理和组合公式即可得到答案.
(1)由题意知,抽出的20名学生中,来自![]() 班的学生有
班的学生有![]() 名.
名.
根据分层抽样的方法可知![]() 班的学生人数估计为
班的学生人数估计为![]() 人.
人.
(2)设从选出的20名学生中任选1人,共有20种选法,
设此人一周上网时长超过15小时为事件D,
其中D包含的选法有3+2+4=9种,所以 ![]() .
.
由此估计从120名学生中任选1名,
该生一周上网时长超过15小时的概率为![]() .
.
(3)设从![]() 班抽出的6名学生中随机选取2人,
班抽出的6名学生中随机选取2人,
其中恰有![]() 人一周上网超过15小时为事件
人一周上网超过15小时为事件![]() ,
,
从![]() 班抽出的7名学生中随机选取1人,
班抽出的7名学生中随机选取1人,
此人一周上网超过15小时为事件![]() ,则所求事件的概率为:
,则所求事件的概率为:
![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A-BCD中,![]() ,点E为棱CD上的一点,且
,点E为棱CD上的一点,且![]() .
.
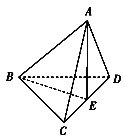
(1)求证:平面![]() 平面BCD;
平面BCD;
(2)若三棱锥A-BCD的体积为![]() ,求三棱锥E-ABD的高.
,求三棱锥E-ABD的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆柱的轴截面ABCD是边长为2的正方形,点P是圆弧CD上的一动点(不与C,D重合),点Q是圆弧AB的中点,且点P,Q在平面ABCD的两侧.
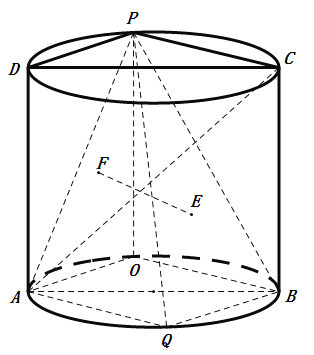
(1)证明:平面PAD⊥平面PBC;
(2)设点P在平面ABQ上的射影为点O,点E,F分别是△PQB和△POA的重心,当三棱锥P﹣ABC体积最大时,回答下列问题.
(i)证明:EF∥平面PAQ;
(ii)求平面PAB与平面PCD所成二面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将曲线![]() 上各点的纵坐标伸长为原来的
上各点的纵坐标伸长为原来的![]() 倍(横坐标不变)得到曲线
倍(横坐标不变)得到曲线![]() ,求
,求![]() 的参数方程;
的参数方程;
(2)若![]() ,
,![]() 分别是直线
分别是直线![]() 与曲线
与曲线![]() 上的动点,求
上的动点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学为了调查该校学生性别与身高的关系,对该校1000名学生按照![]() 的比例进行抽样调查,得到身高频数分布表如下:
的比例进行抽样调查,得到身高频数分布表如下:
男生身高频率分布表
男生身高 (单位:厘米) |
|
|
|
|
|
|
频数 | 7 | 10 | 19 | 18 | 4 | 2 |
女生身高频数分布表
女生身高 (单位:厘米) |
|
|
|
|
|
|
频数 | 3 | 10 | 15 | 6 | 3 | 3 |
(1)估计这1000名学生中女生的人数;
(2)估计这1000名学生中身高在![]() 的概率;
的概率;
(3)在样本中,从身高在![]() 的女生中任取2名女生进行调查,求这2名学生身高在
的女生中任取2名女生进行调查,求这2名学生身高在![]() 的概率.(身高单位:厘米)
的概率.(身高单位:厘米)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)
如图,已知抛物线![]() ,过点
,过点![]() 任作一直线与
任作一直线与![]() 相交于
相交于![]() 两点,过点
两点,过点![]() 作
作![]() 轴的平行线与直线
轴的平行线与直线![]() 相交于点
相交于点![]() (
(![]() 为坐标原点).
为坐标原点).
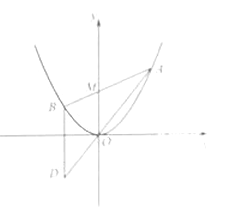
(1)证明:动点![]() 在定直线上;
在定直线上;
(2)作![]() 的任意一条切线
的任意一条切线![]() (不含
(不含![]() 轴)与直线
轴)与直线![]() 相交于点
相交于点![]() ,与(1)中的定直线相交于点
,与(1)中的定直线相交于点![]() ,证明:
,证明:![]() 为定值,并求此定值.
为定值,并求此定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com