(12分)已知函数f(x)=
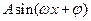
(其中A>0,
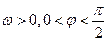
)的图象如图所示。
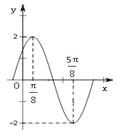
(Ⅰ)求A,w及j的值;
(Ⅱ)若tana=2,求
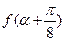
的值。
(1)A=2,w=2,j=
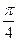
(2)
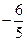
(Ⅰ)由图知A="2, " ……………………1分
T=2(
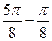
)=p,
∴w="2," ……………………3分
∴f(x)=2sin(2x+j)
又∵
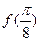
=2sin(
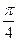
+j)=2,
∴sin(
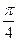
+j)=1,
∴
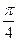
+j=
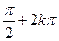
,j=
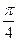
+
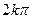
,(kÎZ)
∵
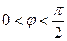
,∴j=
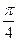
……………………6分
由(Ⅰ)知:f(x)=2sin(2x+
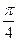
),
∴
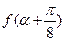
=2sin(2a+
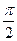
)=2cos2a=4cos
2a-2…………9分
∵tana=2,∴sina=2cosa,
又∵sin
2a+cos
2a=1,∴cos
2a=
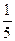
,
∴
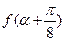
=
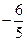
……………………12分
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(本小题满分16分)设函数
f(
x)=
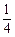 x4
x4+
bx2+
cx+
d,当
x=
t1时,
f(
x)有极小值.
(1)若
b=-6时,函数
f(
x)有极大值,求实数
c的取值范围;
(2)在(1)的条件下,若存在实数
c,使函数
f(
x)在闭区间[
m-2,
m+2]上单调递增,求实数
m的取值范围;
(3)若函数
f(
x)只有一个极值点,且存在
t2∈(
t1,
t1+1),使
f ′(
t2)=0,证明:函数
g(
x)=
f(
x)-
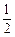 x2
x2+
t1x在区间(
t1,
t2)内最多有一个零点.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
若连续且不恒等于的零的函数
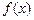
满足
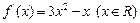
,试写出一个符合题意的函数
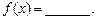
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分12分)已知函数
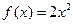
,
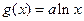
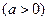
,点
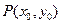
是函数
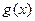
图象上任意一点,直线
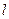
为函数
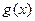
的图象在
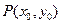
处的切线.
(I)求直线
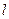
的方程;
(II)若直线
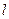
与
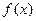
的图象相切,求
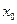
和
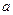
的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
(文)曲线
f(
x)=
x3+
x-2在
p0点处的切线平行于直线
y=4
x-1,则
p0点的坐标为( )
| A.(-1,0) | B.(0,-2) |
| C.(-1,-4)或(1,0) | D.(1,4) |
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
在同一平面直角坐标系中,已知函数
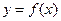
的图象与
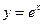
的图象关于直线
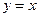
对称,则函数
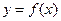
对解析式为
;其应的曲线在点(
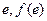
)处的切线方程为
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
过点
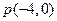
作曲线
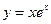
的切线,则切线方程为
。
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
下列结论①当
a<0时,
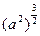
=
a3 ,②
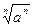
=|
a| ,③函数
y=
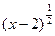
-(3
x-7)
0的定义域是(2, +∞), ④若
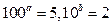
,则2
a+
b=1其中正确的个数是
查看答案和解析>>

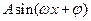 (其中A>0,
(其中A>0,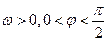 )的图象如图所示。
)的图象如图所示。
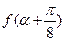 的值。
的值。 阅读快车系列答案
阅读快车系列答案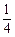 x4+bx2+cx+d,当x=t1时,f(x)有极小值.
x4+bx2+cx+d,当x=t1时,f(x)有极小值.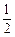 x2+t1x在区间(t1,t2)内最多有一个零点.
x2+t1x在区间(t1,t2)内最多有一个零点.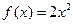 ,
,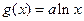
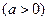 ,点
,点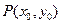 是函数
是函数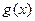 图象上任意一点,直线
图象上任意一点,直线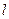 为函数
为函数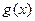 的图象在
的图象在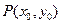 处的切线.
处的切线. 的方程;
的方程; 与
与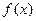 的图象相切,求
的图象相切,求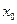 和
和 的取值范围.
的取值范围.