
(1)判断g(x)与M间的关系,并说明理由;
(2)M中的元素是否都是周期函数,证明你的结论;
(3)M中的元素是否都是奇函数,证明你的结论.
思路分析:f(x)是一个抽象函数,g(x)是一个具体函数,(1)就是让我们判断g(x)是否为f(x)的一个“原函数”,也就是说,g(x)是否满足g(x)+g(x+2)=g(x+1);若g(x)∈M,g(x)为周期函数,其周期为6,那么f(x)也应该是周期函数,其周期也应是6.这就为我们解答(2)指明了方向.
解:(1)∵sin![]() x+sin
x+sin![]() (x+2)
(x+2)
=2sin![]() (x+1)cos
(x+1)cos![]() =sin
=sin![]() (x+1),
(x+1),
即g(x)+g(x+2)=g(x+1),
∴g(x)∈M.
(2)∵f(x)+f(x+2)=f(x+1),
∴f(x+1)+f(x+3)=f(x+2),
由此得出f(x+3)+f(x)=0,
即f(x+3)=-f(x).
∴f(x+6)=-f(x+3)=f(x).
这就表明,f(x)是周期函数,其周期为6.
(3)类似(2),可以证明y=cos![]() x也是M中的元素,但y=cos
x也是M中的元素,但y=cos![]() x不是奇函数.
x不是奇函数.


科目:高中数学 来源: 题型:
| 1 |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川眉山市高三上学期一诊测文科数学试卷(解析版) 题型:填空题
已知集合M={f(x)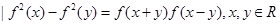 },有下列命题
},有下列命题
①若f(x)=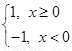 ,则f(x)
,则f(x)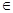 M;
M;
②若f(x)=2x,则f(x)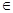 M;
M;
③f(x)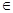 M,则y=f(x)的图像关于原点对称;
M,则y=f(x)的图像关于原点对称;
④f(x)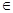 M,则对于任意实数x1,x2(x1
M,则对于任意实数x1,x2(x1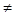 x2),总有
x2),总有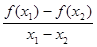 ﹤0成立;
﹤0成立;
其中所有正确命题的序号是_______。(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源:模拟题 题型:填空题
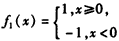 ,则f1(x)∈M;
,则f1(x)∈M;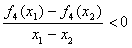 成立;
成立;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com