
如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,已知PB=PD=2,PA=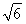 .
.
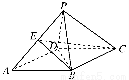
(1)证明:PC⊥BD;
(2)若E为PA的中点,求三棱锥P-BCE的体积.
(1)见解析(2)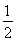
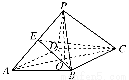
【解析】(1)证明:连接AC,交BD于点O,连接PO.
因为底面ABCD是菱形,所以AC⊥BD,BO=DO.
由PB=PD知,PO⊥BD.
又因为PO∩AC=O,所以BD⊥平面APC.
又PC?平面APC,因此BD⊥PC.
(2)因为E是PA的中点,
所以V三棱锥P-BCE=V三棱锥C-PEB=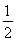 V三棱锥C-PAB=
V三棱锥C-PAB=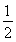 V三棱锥B-APC.
V三棱锥B-APC.
由PB=PD=AB=AD=2知,△ABD≌△PBD.
因为∠BAD=60°,
所以PO=AO=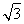 ,AC=2
,AC=2 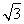 ,BO=1.
,BO=1.
又PA=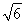 ,所以PO2+AO2=PA2,所以PO⊥AC,
,所以PO2+AO2=PA2,所以PO⊥AC,
故S△APC=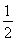 PO·AC=3.
PO·AC=3.
由(1)知,BO⊥平面APC,
因此V三棱锥P-BCE=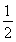 V三棱锥B-APC=
V三棱锥B-APC=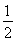 ·
·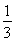 ·BO·S△APC=
·BO·S△APC=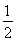 .
.


科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)仿真模拟卷2练习卷(解析版) 题型:选择题
一个由实数组成的等比数列,它的前6项和是前3项和的9倍,则此数列的公比为( )
A.2 B.3 C.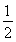 D.
D.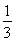
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷6练习卷(解析版) 题型:选择题
某校为了研究学生的性别和对待某一活动的态度(支持和不支持的两种态度)的关系,运用2×2列联表进行独立性检验,经计算K2=7.069,则所得到的统计学结论是:有________的把握认为“学生性别与支持该活动有关系”( )
附:
P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
A.0.1% B.1% C.99% D.99.9%
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷5练习卷(解析版) 题型:选择题
已知直线l过抛物线y2=4x的焦点F,交抛物线于A、B两点,且点A、B到y轴的距离分别为m,n,则m+n+2的最小值为( )
A.4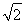 B.6
B.6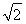 C.4 D.6
C.4 D.6
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷5练习卷(解析版) 题型:选择题
已知点P(3,2)与点Q(1,4)关于直线l对称,则直线l的方程为( )
A.x-y+1=0 B.x-y=0
C.x+y+1=0 D.x+y=0
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷4练习卷(解析版) 题型:选择题
一几何体的三视图如图所示,则该几何体的体积为( )、
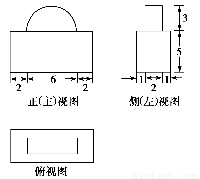
A.200+9π B.200+18π
C.140+9π D.140+18π
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷3练习卷(解析版) 题型:选择题
下列推理中属于归纳推理且结论正确的是( )
A.设数列{an}的前n项和为Sn.由an=2n-1,求出S1=12,S2=22,S3=32,…,推断:Sn=n2
B.由f(x)=xcos x满足f(-x)=-f(x)对?x∈R都成立,推断:f(x)=xcos x为奇函数
C.由圆x2+y2=r2的面积S=πr2,推断:椭圆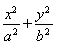 =1(a>b>0)的面积S=πab
=1(a>b>0)的面积S=πab
D.由(1+1)2>21,(2+1)2>22,(3+1)2>23,…,推断:对一切n∈N*,(n+1)2>2n
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(解析版) 题型:选择题
函数y=f(x),x∈D,若存在常数C,对任意的x1∈D,存在唯一的x2∈D使得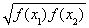 =C,则称函数f(x)在D上的几何平均数为C.已知f(x)=x3,x∈[1,2],则函数f(x)=x3在[1,2]上的几何平均数为( )
=C,则称函数f(x)在D上的几何平均数为C.已知f(x)=x3,x∈[1,2],则函数f(x)=x3在[1,2]上的几何平均数为( )
A. 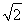 B.2
B.2
C.4 D.2 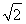
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com