
【题目】若存在![]() ,使得
,使得![]() 对任意
对任意![]() 恒成立,则函数
恒成立,则函数![]() 在
在![]() 上有下界,其中
上有下界,其中![]() 为函数
为函数![]() 的一个下界;若存在
的一个下界;若存在![]() ,使得
,使得![]() 对任意
对任意![]() 恒成立,则函数
恒成立,则函数![]() 在
在![]() 上有上界,其中
上有上界,其中![]() 为函数
为函数![]() 的一个上界.如果一个函数既有上界又有下界,那么称该函数有界.
的一个上界.如果一个函数既有上界又有下界,那么称该函数有界.
下述四个结论:①1不是函数![]() 的一个下界;②函数
的一个下界;②函数![]() 有下界,无上界;③函数
有下界,无上界;③函数![]() 有上界,无下界;④函数
有上界,无下界;④函数![]() 有界.
有界.
其中所有正确结论的编号是( )
A.①②B.②④C.③④D.②
【答案】B
【解析】
根据函数上界、下界及有界的概念,利用导数判断函数的单调性并求最值,结合选项,利用排除法,对结论①②③④进行逐项判断即可.
对于结论①:当![]() 时,由对勾函数的性质知,函数
时,由对勾函数的性质知,函数![]() 恒成立,所以可得函数
恒成立,所以可得函数![]() 对任意
对任意![]() 恒成立,即1是函数
恒成立,即1是函数![]() 的一个下界,故结论①错误;
的一个下界,故结论①错误;
对于结论②:因为函数![]() ,
,![]() ,所以
,所以![]() ,所以当
,所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,故函数
,故函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,所以当
上单调递增,所以当![]() 时,函数
时,函数![]() 有最小值为
有最小值为![]() ,即存在
,即存在![]() 使任意
使任意![]() ,
,![]()
![]() 恒成立,故函数
恒成立,故函数![]() 有下界;当
有下界;当![]() 时,函数
时,函数![]() ,故函数
,故函数![]() 无上界;因此结论②正确;
无上界;因此结论②正确;
对于结论③:因为函数![]() ,所以
,所以![]() ,所以当
,所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;所以函数
;所以函数![]() 在
在![]() 上单调递增;在
上单调递增;在![]() 上单调递减,当
上单调递减,当![]() 时,
时,![]() ,所以函数
,所以函数![]() 无上界,故结论③错误;
无上界,故结论③错误;
对于结论④:因为函数![]() 为周期函数,且
为周期函数,且![]() ,当
,当![]() 时,
时,![]() ,该函数为振荡函数,所以对任意
,该函数为振荡函数,所以对任意![]() 函数
函数![]() 恒成立,故函数
恒成立,故函数![]() 有界,故结论④正确.
有界,故结论④正确.
故选:B


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】某企业有甲、乙两套设备生产同一种产品,为了检测两套设备的生产质量情况,随机从两套设备生产的大量产品中各抽取了50件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内,则为合格品,否则为不合格品. 表1是甲套设备的样本的频数分布表,图1是乙套设备的样本的频率分布直方图.
内,则为合格品,否则为不合格品. 表1是甲套设备的样本的频数分布表,图1是乙套设备的样本的频率分布直方图.
表1:甲套设备的样本的频数分布表
质量指标值 | [95,100) | [100,105) | [105,110) | [110,115) | [115,120) | [120,125] |
频数 | 1 | 5 | 18 | 19 | 6 | 1 |
图1:乙套设备的样本的频率分布直方图
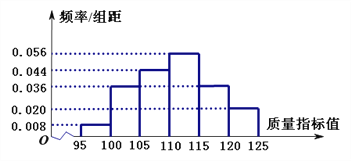
(Ⅰ)将频率视为概率. 若乙套设备生产了5000件产品,则其中的不合格品约有多少件;
(Ⅱ)填写下面列联表,并根据列联表判断是否有90%的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关;
甲套设备 | 乙套设备 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
(Ⅲ)根据表1和图1,对两套设备的优劣进行比较.
附:

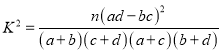 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4 — 4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为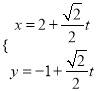 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ).
).
(1)分别写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,若
两点,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() .直线
.直线![]() 被称作为椭圆
被称作为椭圆![]() 的一条准线.点
的一条准线.点![]() 在椭圆
在椭圆![]() 上(异于椭圆左、右顶点),过点
上(异于椭圆左、右顶点),过点![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 相切,且与直线
相切,且与直线![]() 相交于点
相交于点![]() .
.
(1)求证:![]() .
.
(2)若点![]() 在
在![]() 轴的上方,
轴的上方,![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①命题“若![]() ,则
,则![]() ”的逆否命题;
”的逆否命题;
②“![]() ,使得
,使得![]() ”的否定是:“
”的否定是:“![]() ,均有
,均有![]() ”;
”;
③命题“![]() ”是“
”是“![]() ”的充分不必要条件;
”的充分不必要条件;
④![]() :
:![]() ,
,![]() :
:![]() ,
,![]() 且
且![]() 为真命题.
为真命题.
其中真命题的序号是________.(填写所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知矩形ABCD,![]() ,
,![]() ,AF⊥平面ABC,且
,AF⊥平面ABC,且![]() .E为线段DC上一点,沿直线AE将△ADE翻折成
.E为线段DC上一点,沿直线AE将△ADE翻折成![]() ,M为
,M为![]() 的中点,则三棱锥
的中点,则三棱锥![]() 体积的最小值是________.
体积的最小值是________.
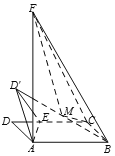
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某数学小组从医院和气象局获得2018年1月至6月份每月20的昼夜温差![]() ,(
,(![]() )和患感冒人数(
)和患感冒人数(![]() /人)的数据,画出如图的折线图.
/人)的数据,画出如图的折线图.
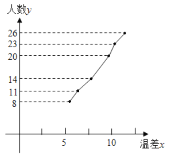
(1)建立![]() 关于
关于![]() 的回归方程(精确到0.01),预测2019年1月至6月份昼夜温差为
的回归方程(精确到0.01),预测2019年1月至6月份昼夜温差为![]() 时患感冒的人数(精确到整数);
时患感冒的人数(精确到整数);
(2)求![]() 与
与![]() 的相关系数,并说明
的相关系数,并说明![]() 与
与![]() 的相关性的强弱(若
的相关性的强弱(若![]() ,则认为
,则认为![]() 与
与![]() 具有较强的相关性),
具有较强的相关性),
参考数据:![]() ,
,![]() ,
,![]() ,
,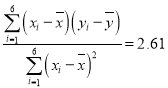 ,
,![]()
相关系数: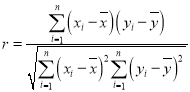 ,回归直线方程是
,回归直线方程是![]() ,
,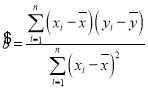 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为贯彻落实党中央全面建设小康社会的战略部署,某贫困地区的广大党员干部深入农村积极开展“精准扶贫”工作.经过多年的精心帮扶,截至2018年底,按照农村家庭人均年纯收入8000元的小康标准,该地区仅剩部分家庭尚未实现小康.2019年7月,为估计该地能否在2020年全面实现小康,统计了该地当时最贫困的一个家庭2019年1至6月的人均月纯收入,作出散点图如下:

根据相关性分析,发现其家庭人均月纯收入![]() 与时间代码
与时间代码![]() 之间具有较强的线性相关关系(记2019年1月、2月……分别为
之间具有较强的线性相关关系(记2019年1月、2月……分别为![]() ,
,![]() ,…,依此类推),由此估计该家庭2020年能实现小康生活.但2020年1月突如其来的新冠肺炎疫情影响了奔小康的进展,该家庭2020年第一季度每月的人均月纯收入均只有2019年12月的预估值的
,…,依此类推),由此估计该家庭2020年能实现小康生活.但2020年1月突如其来的新冠肺炎疫情影响了奔小康的进展,该家庭2020年第一季度每月的人均月纯收入均只有2019年12月的预估值的![]() .
.
(1)求该家庭2020年3月份的人均月纯收人;
(2)如果以该家庭3月份人均月纯收入为基数,以后每月的增长率为![]() ,为使该家庭2020年能实现小康生活,
,为使该家庭2020年能实现小康生活,![]() 至少应为多少?(结果保留两位小数)
至少应为多少?(结果保留两位小数)
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式:线性回归方程![]() 中,
中, ,
,![]() ;
;
![]() (
(![]() ,
,![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com