
【题目】如图,在正三棱柱![]() 中,
中,![]() ,E,F分别为AB,
,E,F分别为AB,![]() 的中点.
的中点.
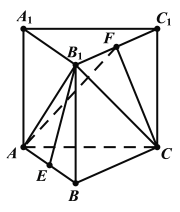
(1)求证:![]() 平面ACF;
平面ACF;
(2)求三棱锥![]() 的体积.
的体积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)取AC的中点M,连结EM,FM,然后利用三角形中位线定理,再结合正棱柱的性质,可得四边形![]() 为平行四边形,从而可得
为平行四边形,从而可得![]() ,再由线面平行定理可证得结果.
,再由线面平行定理可证得结果.
(2)设O为BC的中点,则可证得![]() 平面
平面![]() ,所以
,所以![]() ,然后代入值计算即可.
,然后代入值计算即可.
(1)证明:取AC的中点M,连结EM,FM,
在![]() 中,因为E、M分别为AB,AC的中点,
中,因为E、M分别为AB,AC的中点,
所以![]() 且
且![]()
又F为![]() 的点,
的点,![]() ,
,
所以![]() 且
且![]() ,
,
即![]() 且
且![]() ,
,
故四边形![]() 为平行四边形,所以
为平行四边形,所以![]() .
.
又![]() 平面ACF内,
平面ACF内,![]() 在平面ACF外,
在平面ACF外,
所以![]() 平面ACF.
平面ACF.
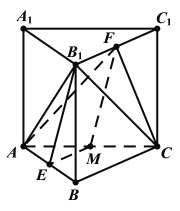
(2)设O为BC的中点,因棱柱底面是正三角形,
所以有![]() ,且
,且![]() ,
,
因为正三棱柱![]() ,
,
所以![]() 平面ABC,
平面ABC,![]() 在平面ABC内,所以
在平面ABC内,所以![]() ,
,
因为![]() ,
,![]() 在平面
在平面![]() 内,
内,
所以![]() 平面
平面![]() .
.
于是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的方程为
的方程为![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 的极坐标方程与直线
的极坐标方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点,求圆
两点,求圆![]() 在
在![]() ,
,![]() 处两条切线的交点坐标.
处两条切线的交点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】哈尔滨市第三中学校响应教育部门疫情期间“停课不停学”的号召,实施网络授课,为检验学生上网课的效果,高三学年进行了一次网络模拟考试.全学年共1500人,现从中抽取了100人的数学成绩,绘制成频率分布直方图(如下图所示).已知这100人中![]() 分数段的人数比
分数段的人数比![]() 分数段的人数多6人.
分数段的人数多6人.
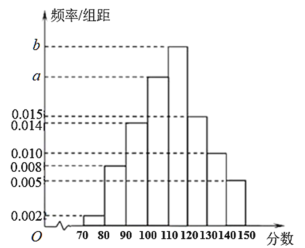
(1)根据频率分布直方图,求a,b的值,并估计抽取的100名同学数学成绩的中位数;
(2)现用分层抽样的方法从分数在![]() ,
,![]() 的两组同学中随机抽取6名同学,从这6名同学中再任选2名同学作为“网络课堂学习优秀代表”发言,求这2名同学的分数不在同一组内的概率.
的两组同学中随机抽取6名同学,从这6名同学中再任选2名同学作为“网络课堂学习优秀代表”发言,求这2名同学的分数不在同一组内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过点
经过点![]() 与直线
与直线![]() 相切,圆心
相切,圆心![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点
,过点![]() 做直线与曲线
做直线与曲线![]() 交于不同两点
交于不同两点![]() ,三角形
,三角形![]() 的垂心为点
的垂心为点![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)求证:点![]() 在一条定直线上,并求出这条直线的方程.
在一条定直线上,并求出这条直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
大学生是国家的未来,代表着国家可持续发展的实力,能够促进国家综合实力的提高.据统计,2016年至2020年我国高校毕业生人数y(单位:万人)的数据如下表:
年份 | 2016 | 2017 | 2018 | 2019 | 2020 |
年份代号x | 16 | 17 | 18 | 19 | 20 |
高校毕业生人数y(单位:万人) | 765 | 795 | 820 | 834 | 874 |
(1)根据上表数据,计算y与x的相关系数r,并说明y与x的线性相关性的强弱.
(已知:![]() ,则认为y与x线性相关性很强;
,则认为y与x线性相关性很强;![]() ,则认为y与x线性相关性一般;
,则认为y与x线性相关性一般;![]() ,则认为y与x线性相关性较弱)
,则认为y与x线性相关性较弱)
(2)求y关于x的线性回归方程,并预测2022年我国高校毕业生的人数(结果取整数).
参考公式和数据: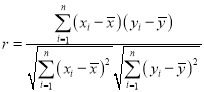 ,
,![]() ,
,![]() ,
,![]() ,
, ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,点P的坐标是![]() ,曲线C的方程为
,曲线C的方程为![]() .以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,斜率为
.以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,斜率为![]() 的直线l经过点P.
的直线l经过点P.
(1)写出直线l的参数方程和曲线C的直角坐标方程;
(2)若直线l和曲线C相交于两点A,B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 经过点
经过点![]() ,且动圆
,且动圆![]() 被
被![]() 轴截得的弦长为4,记圆心
轴截得的弦长为4,记圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的标准方程;
的标准方程;
(2)过![]() 轴下方一点
轴下方一点![]() 向曲线
向曲线![]() 作切线,切点记作
作切线,切点记作![]() 、
、![]() ,直线
,直线![]() 交曲线
交曲线![]() 于点
于点![]() ,若直线
,若直线![]() 、
、![]() 的斜率乘积为
的斜率乘积为![]() ,点
,点![]() 在以
在以![]() 为直径的圆上,求点
为直径的圆上,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
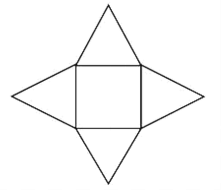
【题目】2020年新型冠状病毒肺炎蔓延全国,作为主要战场的武汉,仅用了十余天就建成了“小汤山”模式的火神山医院和雷神山医院,再次体现了中国速度.随着疫情发展,某地也需要参照“小汤山”模式建设临时医院,其占地是出一个正方形和四个以正方形的边为底边、腰长为400m的等腰三角形组成的图形(如图所示),为使占地面积最大,则等腰三角形的底角为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com