
【题目】已知函数f(x)=|x|,g(x)=﹣|x﹣4|+m.
(1)解关于x的不等式g[f(x)]+3﹣m>0;
(2)若函数f(x)的图象恒在函数g(2x)图象的上方,求实数m的取值范围.
【答案】
(1)解:由g[f(x)]+3﹣m>0得||x|﹣4|<3,
∴﹣3<|x|﹣4<3,
∴1<|x|<7,
故不等式的解集为(﹣7,﹣1)∪(1,7)
(2)解:∵函数f(x)的图象恒在函数g(x)图象的上方
∴f(x)>g(2x)恒成立,
即m<|2x﹣4|+|x|恒成立,
∵|2x﹣4|+|x|= 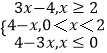 ,
,
∴|2x﹣4|+|x|≥2,
∴m的取值范围为m<2
【解析】(1)问题转化为﹣3<|x|﹣4<3,解出即可;(2)由题意得f(x)>g(2x)恒成立,即m<|2x﹣4|+|x|恒成立,通过讨论x的范围求出m的范围即可.
【考点精析】解答此题的关键在于理解绝对值不等式的解法的相关知识,掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log4(4x+1)﹣ ![]() x.
x.
(1)试判断函数f(x)的奇偶性并证明;
(2)设g(x)=log4(a2x﹣ ![]() a),若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
a),若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 在
在![]() 单调递增,其中
单调递增,其中![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,当
,当![]() 时,试比较
时,试比较![]() 与
与![]() 的大小关系(其中
的大小关系(其中![]() 是
是![]() 的导函数),请写出详细的推理过程;
的导函数),请写出详细的推理过程;
(3)当![]() 时,
时, ![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在空间直角坐标系中,已知A(3,0,1)和B(1,0,-3),试问
(1)在y轴上是否存在点M,满足 ![]() ?
?
(2)在y轴上是否存在点M,使△MAB为等边三角形?若存在,试求出点M坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海滨游乐场出租快艇的收费办法如下:不超过十分钟收费80元;超过十分钟,超过部分按每分钟10元收费(对于其中不足一分钟的部分,若小于0.5分钟则不收费,若大于或等于0.5分钟则按一分钟收费),小茗同学为该游乐场设计了一款收费软件,程序框图如图所示,其中x(分钟)为航行时间,y(元)为所收费用,用[x]表示不大于x的最大整数,则图中①处应填( ) 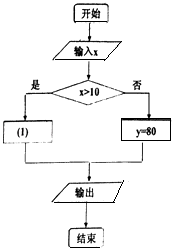
A.y=10[x]
B.y=10[x]﹣20
C.y=10[x﹣ ![]() ]﹣20
]﹣20
D.y=10[x+ ![]() ]﹣20
]﹣20
查看答案和解析>>
科目:高中数学 来源: 题型:
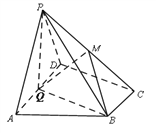
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,平面
,平面![]() 底面ABCD,Q为AD的中点,M是棱
底面ABCD,Q为AD的中点,M是棱![]() 上的点,
上的点, ![]()
(Ⅰ)若![]() 是棱
是棱![]() 的中点,求证:
的中点,求证: ![]() ;
;
(Ⅱ)若二面角![]() 的大小为
的大小为![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com