
【题目】已知函数![]() 有极值,且导函数
有极值,且导函数![]() 的极值点是
的极值点是![]() 的零点,给出命题:①
的零点,给出命题:①![]() ;②若
;②若![]() ,则存在
,则存在![]() ,使得
,使得![]() ;③若
;③若![]() 有两个极值点
有两个极值点![]() ,
,![]() ,则
,则![]() ;④若
;④若![]() ,且
,且![]() 是曲线
是曲线![]() ,
,![]() 的一条切线,则
的一条切线,则![]() 的取值范围是
的取值范围是![]() ;则以上命题正确序号是______.
;则以上命题正确序号是______.
【答案】①②④
【解析】
由函数有极值,求得![]() 的范围,同时有导函数
的范围,同时有导函数![]() 的极值点是
的极值点是![]() 的零点求得
的零点求得![]() 的关系,判断四个命题的真假,其中①由刚才的关系式就可判断,②用导数研究函数的单调性,结合零点存在定理可得,③可举反例说明,④用已知得出
的关系,判断四个命题的真假,其中①由刚才的关系式就可判断,②用导数研究函数的单调性,结合零点存在定理可得,③可举反例说明,④用已知得出![]() 在
在![]() 单调性,化简函数,利用导数的几何意义求出
单调性,化简函数,利用导数的几何意义求出![]() 的表达式,从而求得其取值范围.
的表达式,从而求得其取值范围.
由题意![]() ,
,![]() ,即
,即![]() .
.
设![]() ,则
,则![]() ,由
,由![]() 得
得![]() ,由
,由![]() 是一次函数知
是一次函数知![]() 是
是![]() 的极值点(本题是极小值点),即为
的极值点(本题是极小值点),即为![]() 的极值点,
的极值点,
所以![]() ,即
,即![]() .
.
①![]() ,①正确;
,①正确;
②显然![]() 时,
时,![]() ,
,
设![]() 的两解为
的两解为![]() ,即为
,即为![]() 的两个极值点,则
的两个极值点,则![]() ,
,![]() 中有一个小于1,一个大于1,不妨设
中有一个小于1,一个大于1,不妨设![]() ,
,![]() 是极大值,而
是极大值,而![]() ,若
,若![]() ,则
,则![]() ,
,![]() 在
在![]() 上在一个零点
上在一个零点![]() ,当
,当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,![]() ,因此
,因此![]() 在
在![]() 上有零点
上有零点![]() .
.
所以![]() 且
且![]() .②正确;
.②正确;
③若![]() ,则极值为0和2,
,则极值为0和2,![]() ,③错误;
,③错误;
④由![]() ,知②中
,知②中![]() ,因此
,因此![]() 在
在![]() 上递增,
上递增,![]() ,
,
![]() ,
,![]() ,设切点为
,设切点为![]() ,
,
则![]() ,即
,即![]() ,整理得
,整理得![]() ,
,
![]() ,因为
,因为![]() ,所以
,所以![]() ,又
,又![]() ,解得
,解得![]() ,
,
![]()
![]()
![]() ,
,
由上知![]() 是增函数,所以当
是增函数,所以当![]() 时,
时,![]() .④正确.
.④正确.
故答案为:①②④.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l的参数方程为![]() (t为参数,0).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数,0).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(Ⅰ)写出曲线C的直角坐标方程;
(Ⅱ)若直线l与曲线C交于A,B两点,且AB的长度为2![]() ,求直线l的普通方程.
,求直线l的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着网络的发展,网上购物越来越受到人们的喜爱,各大购物网站为增加收入,促销策略越来越多样化,促销费用也不断增加.下表是某购物网站2018年1月~8月促销费用(万元)和产品销量(万件)的具体数据.
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
促销费用 | 2 | 3 | 6 | 10 | 13 | 21 | 15 | 18 |
产品销量 | 1 | 1 | 2 | 3 | 3.5 | 5 | 4 | 4.5 |
(1)根据数据可知![]() 与
与![]() 具有线性相关关系,请建立
具有线性相关关系,请建立![]() 与
与![]() 的回归方程
的回归方程![]() (系数精确到0.01);
(系数精确到0.01);
(2)已知6月份该购物网站为庆祝成立1周年,特制定奖励制度:以![]() (单位:件)表示日销量,
(单位:件)表示日销量,![]() ,则每位员工每日奖励100元;
,则每位员工每日奖励100元;![]() ,则每位员工每日奖励150元,
,则每位员工每日奖励150元,![]() ,则每位员工每日奖励200元.现已知该网站6月份日销量
,则每位员工每日奖励200元.现已知该网站6月份日销量![]() 服从正态分布
服从正态分布![]() ,请你计算某位员工当月奖励金额总数大约多少元(当月奖励金额总数精确到百分位).
,请你计算某位员工当月奖励金额总数大约多少元(当月奖励金额总数精确到百分位).
参考数据:![]() ,
,![]() ,其中
,其中![]() ,
,![]() 分别为第
分别为第![]() 个月的促销费用和产品销量,
个月的促销费用和产品销量,![]() .
.
参考公式:①对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为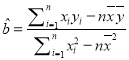 ,
,![]() ;②若随机变量
;②若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是抛物线
是抛物线![]() 的焦点,过点
的焦点,过点![]() 且与坐标轴不垂直的直线交抛物线于
且与坐标轴不垂直的直线交抛物线于![]() 、
、![]() 两点,交抛物线的准线于点
两点,交抛物线的准线于点![]() ,其中
,其中![]() ,
,![]() .过点
.过点![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,直线
,直线![]() 交抛物线于点
交抛物线于点![]() .
.
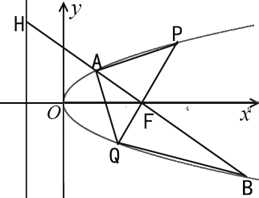
(1)求![]() 的值;
的值;
(2)求四边形![]() 的面积
的面积![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为2,过点
的焦距为2,过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设椭圆的右焦点为F,定点![]() ,过点F且斜率不为零的直线l与椭圆交于A,B两点,以线段AP为直径的圆与直线
,过点F且斜率不为零的直线l与椭圆交于A,B两点,以线段AP为直径的圆与直线![]() 的另一个交点为Q,证明:直线BQ恒过一定点,并求出该定点的坐标.
的另一个交点为Q,证明:直线BQ恒过一定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,
为正方形,![]() 平面
平面![]() ,
,![]() ,
,![]() 为
为![]() 上异于
上异于![]() 的点.
的点.
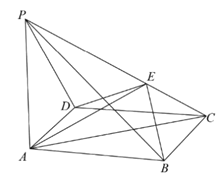
(1)求证:平面![]() 平面
平面![]() ;
;
(2)当![]() 与平面
与平面![]() 所成角为
所成角为![]() 时,求
时,求![]() 的长;
的长;
(3)当![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率
的离心率![]() ,且圆
,且圆![]() 过椭圆
过椭圆![]() 的上,下顶点.
的上,下顶点.
(1)求椭圆![]() 的方程.
的方程.
(2)若直线![]() 的斜率为
的斜率为![]() ,且直线
,且直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,点
两点,点![]() 关于点的对称点为
关于点的对称点为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上一点,判断直线
上一点,判断直线![]() 与
与![]() 的斜率之和是否为定值,如果是,请求出此定值:如果不是,请说明理.
的斜率之和是否为定值,如果是,请求出此定值:如果不是,请说明理.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com