
����Ŀ���ڹ᳹�й��������Ժ���ھ���ƶ���ߵĹ����У�ij��λ������100��ƶ����.���������100�������ƶ��״���ͼ�ͥ��Ա�ܽ�����������˵��飺�״�55��ƶ�������У���ͥ��Ա���ܹ��еȼ����Ͻ�����ֻ��10�����Ҵ�45��ƶ�������У���ͥ��Ա���ܹ��еȼ����Ͻ�������20��.
��1���������������������ж��Ƿ���99.5%�İ�����Ϊƶ������ܽ�������йأ�
��ͥ��Ա���ܹ��е����� �����Ļ��� | ��ͥ��Ա���ܹ��еȼ����� �����Ļ��� | �ϼ� | |
�״�ƶ������ | |||
�Ҵ�ƶ������ | |||
�ϼ� |
��2���ڱ������100��ƶ�����У����ֲ�����ķ����Ӽ�ͥ��Ա���ܹ��еȼ����Ͻ�����ƶ�����г�ȡ6�����ٴ���6���в��ü���������ķ��������ȡ2��������2���мס�������ǡ�ø�1���ĸ���.
�ο���ʽ�����ݣ�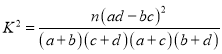 ������
������![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���𰸡���1�����������������а��գ���2��![]()
��������
��1��������������������д�����������ݹ�ʽ����![]() ��ֵ�����½��ۣ�
��ֵ�����½��ۣ�
��2�����ݷֲ�����ij����ȵó������ȡ���������ùŵ����������.
��1���������е����ݣ���д���������£�
��ͥ��Ա���ܹ��е����� �����Ļ��� | ��ͥ��Ա���ܹ��еȼ����� �����Ļ��� | �ϼ� | |
�״�ƶ������ | 45 | 10 | 55 |
�Ҵ�ƶ������ | 25 | 20 | 45 |
�ϼ� | 70 | 30 | 100 |
��Ϊ![]() ��
��
������99.5%�İ�����Ϊƶ������ܽ�������й�.
��2���������⣬�ڳ�ȡ��6���У��Ҵ�4�����״�2����
�ֱ���Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
����6���������ȡ2���õ��������ռ�Ϊ
![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
�����ռ�����15��
������2����ǡ��Ϊ1���״塢1���Ҵ����������8��
�����2����ǡ��Ϊ1���״塢1���Ҵ�ĸ�����![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �ڶ�����
�ڶ�����![]() �ڵ�ij������
�ڵ�ij������![]() ��������������
��������������![]() ��
��![]() ��Ҳ�������������
��Ҳ�������������![]() ��
��![]() �ϵ���������������.��֪
�ϵ���������������.��֪![]() ��
��![]() .
.
��1���жϺ���![]() �Ƿ�Ϊ����
�Ƿ�Ϊ����![]() �ϵġ���������������
�ϵġ���������������
��2��������![]() ������
������![]() �ϵġ�����������������ʵ��
�ϵġ�����������������ʵ��![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �IJ���ͼ����ͼ��ʾ.
�IJ���ͼ����ͼ��ʾ.
��1����![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����![]() �ĵ����ݼ����䣻
�ĵ����ݼ����䣻
��3������ͼ��˵������![]() ��ͼ�������ı任�ɵõ�
��ͼ�������ı任�ɵõ�![]() ��ͼ��.
��ͼ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() �У�
�У� ![]() ���ഹֱ��
���ഹֱ�� ![]() ��
�� ![]() ���߶�
���߶�![]() ��һ���㣬��ֱ��
��һ���㣬��ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ����е����ֵ��
���ɽǵ����е����ֵ��![]() ��������
��������![]() �������ı�����ǣ�������
�������ı�����ǣ�������
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
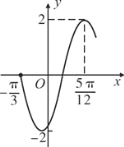
����Ŀ��2019��ȫ�������ᡱ�����л�������ʮ����ȫ���˴���λ�����й���������Э�̻����ʮ����ȫ��ίԱ��ڶ��λ��飬�ֱ���2019��3��5�պ�3��3���ڱ����ٿ�Ϊ���˽���Щ�˸���ע�����ᡱ��ij���������ȡ��������15~75��֮���200�˽��е��飬����������Ƶ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ����������������![]() ��
��![]() �ڵ��˷ֱ��Ϊ���������ˡ��͡��������ˡ���ͳ�ơ��������ˡ��͡��������ˡ�������֮��Ϊ
�ڵ��˷ֱ��Ϊ���������ˡ��͡��������ˡ���ͳ�ơ��������ˡ��͡��������ˡ�������֮��Ϊ![]() .���С��������ˡ�����40�˹�ע�����ᡱ�����������ˡ��й�ע�����ᡱ�Ͳ���ע�����ᡱ������֮����
.���С��������ˡ�����40�˹�ע�����ᡱ�����������ˡ��й�ע�����ᡱ�Ͳ���ע�����ᡱ������֮����![]() .
.

��1����ͼ��![]() ��ֵ������÷ֲ������
��ֵ������÷ֲ������![]() ��
��![]() �������ȡ8����������8���Ё�ѡ2�ˣ���2����������1���ǡ��������ˡ��ĸ����Ƕ��٣�
�������ȡ8����������8���Ё�ѡ2�ˣ���2����������1���ǡ��������ˡ��ĸ����Ƕ��٣�
��2��������֪��������������![]() �������������ݴ�ͳ�ƽ���жϣ��ܷ���
�������������ݴ�ͳ�ƽ���жϣ��ܷ���![]() �İ�����Ϊ���������ˡ��ȡ��������ˡ����ӹ�ע�����ᡱ��
�İ�����Ϊ���������ˡ��ȡ��������ˡ����ӹ�ע�����ᡱ��
��ע | ����ע | �ϼ� | |
�������� | |||
�������� | |||
�ϼ� |
�ο����ݼ���ʽ��
| 0.150 | 0.100 | 0.050 | 0.010 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 10.828 |

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ӵ�ý��˾Ϊ���˽�ij�������ӹ��ڶ�ij��������Ŀ����������������ȡ��100�����ڽ��е��飬����Ů����55���������Ǹ��ݵ��������ƵĹ����վ��տ���������Ŀʱ���Ƶ�ʷֲ�ֱ��ͼ��
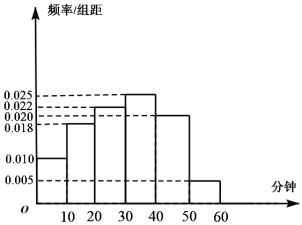
���վ��տ���������Ŀʱ�䲻����40���ӵĹ��ڳ�Ϊ��������������֪��������������10��Ů�ԣ�
(��)������֪������������![]() �����������ݴ��������Ƿ���Ϊ�������������Ա�
�����������ݴ��������Ƿ���Ϊ�������������Ա�
�йأ�
�������� | ������ | �ϼ� | |
�� | |||
Ů | |||
�ϼ� |
(��)���վ��տ���������Ŀ������50���ӵĹ��ڳ�Ϊ������������������֪������������������2��Ů�ԣ�������������������������ѡȡ2�ˣ���������1��Ů�Թ��ڵĸ��ʣ�
| 0.05 | 0.01 |
k | 3.841 | 6.635 |
��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x����axlnx��x2��ax+1��a��R���ڶ���������������ͬ�ļ�ֵ��.
��1����ʵ��a��ȡֵ��Χ��
��2����������ֵ��ֱ�Ϊx1��x2��x1��x2��֤����f��x1��+f��x2����2��x12+x22.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʡ�����ػ�Į����Ϊ���ص�ʡ�ݣ�һ������ɳ��Ϊ�˹�ɳ����ɳ��������̬���������ϵؽ����о���ʵ����ʵ����ɳ���˽���2019�꣬�����ذ˲�ɳ�ֳ������Ϻ�����������ɳȺ����Ϊ��������������������衰ʱ����ģ���ƺţ�����ɳ������Ϊ���ij�ֹ�ɳ������Ч������ɳ����ijһʵ��ɳ����¶���������������50����ʴ��ǥ���Բ�����ʴֵ����ʴֵ�Dz�����ɳЧ����ָ��֮һ����ֵԽС��ʾ�ò�ǥ�����紵�ߵ�ɳ����ԽС��˵����ɳЧ��Խ�ã���ֵΪ0��ʾ�ò��봦û�б���ʴ��ͨ��һ��ʱ��Ĺ۲⣬��ɳ�˼�¼���¶�������ȫ����ǥ��õķ�ʴֵ���������ݾ���Ϊ������������������Ӧ��Ƶ�ʷֲ�ֱ��ͼ��

������ֱ��ͼ���ơ�������һ����ǥ��ʴֵС��30���ĸ��ʣ�
������һ����ǥ�ķ�ʴֵС��30���������Ҫ��ǡ�*��������ǣ���������ֱ��ͼ�������������
��� | ����� | �ϼ� | |
���� | |||
�¶� | |||
�ϼ� |
���ж��Ƿ���![]() �İ�����Ϊ���ݱ�ǡ�*����ɳ���ϲ�ǥ�������λ���й�?
�İ�����Ϊ���ݱ�ǡ�*����ɳ���ϲ�ǥ�������λ���й�?
�����¶���������ƽ����ʴֵ�ֱ�Ϊ![]() ��
��![]() ����
����![]() �������Ϊ�˹�ɳ�������¶��������Ĺ�ɳЧ�����ڲ��죬�Ը���ֱ��ͼ����
�������Ϊ�˹�ɳ�������¶��������Ĺ�ɳЧ�����ڲ��죬�Ը���ֱ��ͼ����![]() ��
��![]() ��ͬһ���е������ø���������е�ֵΪ�����������жϸù�ɳ�������¶��������Ĺ�ɳЧ���Ƿ���ڲ��죮
��ͬһ���е������ø���������е�ֵΪ�����������жϸù�ɳ�������¶��������Ĺ�ɳЧ���Ƿ���ڲ��죮
����
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ƽ��![]() ƽ��ABC��P��P��ƽ��ABC��ͬ�࣬�����
ƽ��ABC��P��P��ƽ��ABC��ͬ�࣬�����![]() ��ƽ���Ϊ�۽ǣ�Q��ƽ��ABC�ľ���Ϊ
��ƽ���Ϊ�۽ǣ�Q��ƽ��ABC�ľ���Ϊ![]() ��
��![]() �DZ߳�Ϊ2���������Σ�
�DZ߳�Ϊ2���������Σ�![]() ��
��![]() ��
��![]() .
.
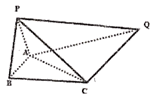
��1����֤����![]() ƽ��PAB��
ƽ��PAB��
��2��������![]() ��ƽ��ǵ�����ֵ.
��ƽ��ǵ�����ֵ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com