
 是否为定值,如果是,请求出定值,如果不是,请说明理由.
是否为定值,如果是,请求出定值,如果不是,请说明理由.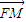 =(
=( ,
, -
-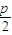 ),
), =(x2-x1,y2-y1)=(x2-x1,
=(x2-x1,y2-y1)=(x2-x1,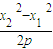 ),的坐标,求其内积即可.
),的坐标,求其内积即可.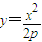 ,故
,故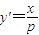 ,切线AM的方程为
,切线AM的方程为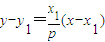 ,即
,即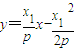 ①,
①,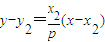 即
即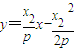 ②
②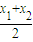 ,
, )
) ),
), =(
=(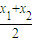 ,
,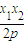 -
-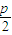 ),
), =(x2-x1,y2-y1)=(x2-x1,
=(x2-x1,y2-y1)=(x2-x1,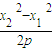 ),
),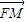 •
•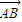 =
=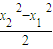 +(
+(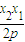 -
- )
)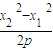 ③
③ ,将y1=
,将y1=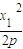 ,
,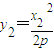 代入整理得x1x2=-p2④,
代入整理得x1x2=-p2④,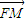 •
•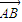 =0
=0 AB×FM=
AB×FM= (
( ,
,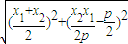 )=
)= (
(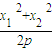 +p)
+p)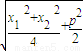
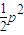


 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:
 (2011•合肥三模)已知抛物线C的方程为x2=2py(p>0),过抛物线上点M(-2
(2011•合肥三模)已知抛物线C的方程为x2=2py(p>0),过抛物线上点M(-2| p |
| p |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:黑龙江省大庆实验中学2010-2011学年高二上学期期末考试数学理科试题 题型:013
已知抛物线x2=2py(p>0),过点![]() 向抛物线引两条切线,A、B为切点,则线段AB的长度是
向抛物线引两条切线,A、B为切点,则线段AB的长度是
2p
p
![]()
![]()
查看答案和解析>>
科目:高中数学 来源:广东省广州市2007年高三年级六校联考数学理科试卷 题型:044
已知抛物线x2=2py(p>0),过动点M(0,a),且斜率为1的直线L与该抛物线交于不同两点A、B,|AB|≤2p,
(1)求a的取值范围;
(2)若p=2,a=3,求直线L与抛物线所围成的区域的面积;
查看答案和解析>>
科目:高中数学 来源:2010年江西省名校高考信息卷一(理) 题型:选择题
已知抛物线x2 = 2py (p > 0),过点M (0 , - )向抛物线引两条切线,A、B为切点,则线段
AB的长度是
|
A.2p |
B.p |
C. |
D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com