
【题目】某学校食堂早餐只有花卷、包子、面条和蛋炒饭四种主食可供食用,有5名同学前去就餐,每人只选择其中一种,且每种主食都至少有一名同学选择.已知包子数量不足仅够一人食用,甲同学肠胃不好不会选择蛋炒饭,则这5名同学不同的主食选择方案种数为________.(用数字作答)
【答案】132
【解析】
分类讨论:甲选包子,则有2人选同一种主食,剩下2人选其余主食;甲不选包子,其余4人中1人选包子,方法为4种,甲花卷或面条,方法为2种,其余3人,有1人选甲选的主食,剩下2人选其余主食,或没有人选甲选的主食,相加后得到结果.
分类讨论:甲选包子,则有2人选同一种主食,方法为![]() =18,
=18,
剩下2人选其余主食,方法为![]() =2,共有方法18×2=36种;
=2,共有方法18×2=36种;
甲不选包子,其余4人中1人选包子,方法为4种,甲花卷或面条,方法为2种,其余3人,
若有1人选甲选的主食,剩下2人选其余主食,方法为3![]() =6;
=6;
若没有人选甲选的主食,方法为![]() =6,共有4×2×(6+6)=96种,
=6,共有4×2×(6+6)=96种,
故共有36+96=132种,
故答案为:132.


科目:高中数学 来源: 题型:
【题目】已知在直角坐标系![]() 中, 直线
中, 直线![]() 的参数方程为是
的参数方程为是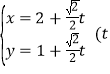 为参数), 以坐标原点
为参数), 以坐标原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系, 曲线
轴正半轴为极轴建立极坐标系, 曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1) 判断直线![]() 与曲线
与曲线![]() 的位置关系;
的位置关系;
(2) 在曲线![]() 上求一点
上求一点![]() ,使得它到直线
,使得它到直线![]() 的距离最大,并求出最大距离.
的距离最大,并求出最大距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地区观众对大型综艺活动《中国好声音》的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众收看该节目的场数与所对应的人数表:
场数 | 9 | 10 | 11 | 12 | 13 | 14 |
人数 | 10 | 18 | 22 | 25 | 20 | 5 |
将收看该节目场次不低于13场的观众称为“歌迷”,已知“歌迷”中有10名女性.
(1)根据已知条件完成下面的2×2列联表,并据此资料我们能否有95%的把握认为“歌迷”与性别有关?
非歌迷 | 歌迷 | 合计 | |
男 | |||
女 | |||
合计 |
(2)将收看该节目所有场次(14场)的观众称为“超级歌迷”,已知“超级歌迷”中有2名女性,若从“超级歌迷”中任意选取2人,求至少有1名女性观众的概率.
P(K2≥k) | 0.05 | 0.01 |
k | 3.841 | 6.635 |
附:K2=![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)
设函数![]() ,其中
,其中![]() .
.
( I )若函数![]() 图象恒过定点P,且点P在
图象恒过定点P,且点P在![]() 的图象上,求m的值;
的图象上,求m的值;
(Ⅱ)当![]() 时,设
时,设![]() ,讨论
,讨论![]() 的单调性;
的单调性;
(Ⅲ)在(I)的条件下,设![]() ,曲线
,曲线![]() 上是否存在两点P、Q,
上是否存在两点P、Q,
使△OPQ(O为原点)是以O为直角顶点的直角三角形,且该三角形斜边的中点在y轴上?如果存在,求a的取值范围;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年6月19日凌晨某公司公布的年中促销全天交易数据显示,天猫年中促销当天全天下单金额为1592亿元.为了了解网购者一次性购物情况,某统计部门随机抽查了6月18日100名网购者的网购情况,得到如下数据统计表,已知网购金额在2000元以上(不含2000元)的频率为0.4.

网购金额(元) | 频数 | 频率 |
| 5 | 0.05 |
|
|
|
| 15 | 0.15 |
| 25 | 0.25 |
| 30 | 0.3 |
|
|
|
合计 | 100 | 1 |
(Ⅰ)先求出![]() 的值,再将图中所示的频率分布直方图绘制完整;
的值,再将图中所示的频率分布直方图绘制完整;
(Ⅱ)对这100名网购者进一步调查显示:购物金额在2000元以上的购物者中网龄3年以上的有35人,购物金额在2000元以下(含2000元)的购物者中网龄不足3年的有20人,请填写下面的列联表,并据此判断能否在犯错误的概率不超过0.025的前提下认为网购金额超过2000元与网龄在3年以上有关?
网龄3年以上 | 网龄不足3年 | 总计 | |
购物金额在2000元以上 | 35 | ||
购物金额在2000元以下 | 20 | ||
总计 | 100 |
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() 其中
其中![]() .
.
(Ⅲ)从这100名网购者中根据购物金额分层抽出20人给予返券奖励,为进一步激发购物热情,在![]() 和
和![]() 两组所抽中的8人中再随机抽取2人各奖励1000元现金,求
两组所抽中的8人中再随机抽取2人各奖励1000元现金,求![]() 组获得现金奖的数学期望.
组获得现金奖的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在实数集上的函数f(x)=x2+ax(a为常数),g(x)= ![]() x3﹣bx+m(b为常数),若函数f(x)在x=1处的切线斜率为3,x=
x3﹣bx+m(b为常数),若函数f(x)在x=1处的切线斜率为3,x= ![]() 是g(x)的一个极值点
是g(x)的一个极值点
(1)求a,b的值;
(2)若存在x∈[﹣4,4]使得f(x)≥g(x)成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}是以d(d≠0)为公差的等差数列,a1=2,且a2 , a4 , a8成等比数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=an2n(n∈N*),求数列{bn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com