
分析 由类比推理的规则得出结论,本题中所用来类比的函数是一个变化率越来越大的函数,而要研究的函数是一个变化率越来越小的函数,其类比方式可知.
解答 解:由题意知,点A、B是函数y=x2的图象上任意不同两点,函数是变化率逐渐变大的函数,线段AB总是位于A、B两点之间函数图象的上方,因此有结论$\frac{{x}_{1}^{2}+{x}_{2}^{2}}{2}$>$\frac{({x}_{1}+{x}_{2})^{2}}{2}$成立;
而函数y=sinx(x∈(0,π))其变化率逐渐变小,线段AB总是位于A、B两点之间函数图象的下方,故可类比得到结论$\frac{sin{x}_{1}+sin{x}_{2}}{2}$<sin$\frac{{x}_{1}+{x}_{2}}{2}$.
故答案为:$\frac{sin{x}_{1}+sin{x}_{2}}{2}$<sin$\frac{{x}_{1}+{x}_{2}}{2}$.
点评 本题考查类比推理,求解本题的关键是理解类比的定义,及本题类比的对象之间的联系与区别,从而得出类比结论.


科目:高中数学 来源: 题型:填空题
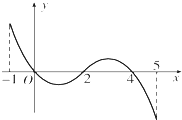 已知函数f(x)的定义域为[-1,5],f(x)的导函数f′(x)的图象如图所示.若f(x)在区间[m,m+1]上是单调函数,则实数m的取值范围是{m|m=-1或0≤m≤1或2≤m≤3或m=4}.
已知函数f(x)的定义域为[-1,5],f(x)的导函数f′(x)的图象如图所示.若f(x)在区间[m,m+1]上是单调函数,则实数m的取值范围是{m|m=-1或0≤m≤1或2≤m≤3或m=4}.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\left\{{\begin{array}{l}{x=sinφ}\\{y={{cos}^2}φ}\end{array}}\right.$(φ为参数) | B. | $\left\{\begin{array}{l}{x=cosφ}\\{y=si{n}^{2}φ}\end{array}\right.$(φ为参数) | ||
| C. | $\left\{\begin{array}{l}{x=\sqrt{1-r}}\\{y=r}\end{array}\right.$(r为参数) | D. | $\left\{\begin{array}{l}{x=tanφ}\\{y=1-ta{n}^{2}φ}\end{array}\right.$(φ为参数) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com