
【题目】解关于![]() 的不等式
的不等式![]() .
.
【答案】当0<a<1时,解集为{x|x<1或x![]() };
};
当a=1时,解集为{x|x≠1};当a>1时,解集为{x|x![]() 或x>1}.
或x>1}.
【解析】
根据a大于1,a=1及a大于0小于1分三种情况取解集,当a大于1时,根据![]() 小于1,利用不等式取解集的方法求出解集;当a=1时,根据完全平方式大于0,得到x不等于1;当a大于0小于1时,根据
小于1,利用不等式取解集的方法求出解集;当a=1时,根据完全平方式大于0,得到x不等于1;当a大于0小于1时,根据![]() 大于1,利用不等式取解集的方法即可求出解集,综上,写出a不同取值时,各自的解集即可.
大于1,利用不等式取解集的方法即可求出解集,综上,写出a不同取值时,各自的解集即可.
由不等式得:![]()
(1)当![]() 时,
时,![]()
原不等式为:![]()
∴不等式的解集为:![]()
(2)当![]() 时,
时,![]()
原不等式为:![]()
![]()
∵![]()
∴不等式的解集为:{x|x<1或x![]() };
};
(3)当![]() 时,
时,![]()
原不等式为:![]()
![]()
∵![]() ,
,
∴不等式的解集为:{x|x![]() 或x>1},
或x>1},
综上所述,得原不等式的解集为:
当0<a<1时,解集为{x|x<1或x![]() };
};
当a=1时,解集为{x|x≠1};当a>1时,解集为{x|x![]() 或x>1}.
或x>1}.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
: ![]() 的离心率是
的离心率是![]() ,且直线
,且直线![]() :
: ![]() 被椭圆
被椭圆![]() 截得的弦长为
截得的弦长为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若直线![]() 与圆
与圆![]() :
: ![]() 相切:
相切:
(i)求圆![]() 的标准方程;
的标准方程;
(ii)若直线![]() 过定点
过定点![]() ,与椭圆
,与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,与圆
,与圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在空间直角坐标系Oxyz中,已知A(2,0,0),B(2,2,0),C(0,2,0),D(1,1, ![]() ),若S1 , S2 , S3分别表示三棱锥D﹣ABC在xOy,yOz,zOx坐标平面上的正投影图形的面积,则( )
),若S1 , S2 , S3分别表示三棱锥D﹣ABC在xOy,yOz,zOx坐标平面上的正投影图形的面积,则( )
A.S1=S2=S3
B.S2=S1且S2≠S3
C.S3=S1且S3≠S2
D.S3=S2且S3≠S1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形AMDE的边长为2,B,C分别为AM,MD的中点,在五棱锥P﹣ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于点G,H. 
(1)求证:AB∥FG;
(2)若PA⊥底面ABCDE,且PA=AE,求直线BC与平面ABF所成角的大小,并求线段PH的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆的中心为原点O,长轴在x轴上,离心率 ![]() ,过左焦点F1作x轴的垂线交椭圆于A、A′两点,|AA′|=4.
,过左焦点F1作x轴的垂线交椭圆于A、A′两点,|AA′|=4. 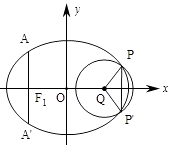
(1)求该椭圆的标准方程;
(2)取垂直于x轴的直线与椭圆相交于不同的两点P、P′,过P、P′作圆心为Q的圆,使椭圆上的其余点均在圆Q外.若PQ⊥P'Q,求圆Q的标准方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com