【题目】已知等差数列{an}的前n项和为Sn ， 公差d≠0，且S3+S5=50，a1 ， a4 ， a13成等比数列．
（1）求数列{an}的通项公式；
（2）设{ 
}是首项为1公比为2的等比数列，求数列{bn}前n项和Tn ．
【答案】
（1）解：∵等差数列{an}的前n项和为Sn，公差d≠0，
且S3+S5=50，a1，a4，a13成等比数列．
∴ 
，
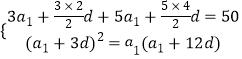解得 
∴an=a1+（n﹣1）d=3+2（n﹣1）=2n+1，
∴an=2n+1
（2）解：∵{ 
}是首项为1公比为2 的等比数列，
∴ 
∴ 
① 
②
两式相减得：
=1+（2n﹣1）2n
【解析】（1）由已知条件利用等差数列的前n项和公式和通项公式以及等比数列的性质，求出首项和公差，由此能求出an=2n+1．（2） ，由此利用错位相减法能求出数列{bn}前n项和Tn ．
【考点精析】利用数列的前n项和对题目进行判断即可得到答案，需要熟知数列{an}的前n项和sn与通项an的关系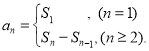
．
轻松夺冠全能掌控卷系列答案科目：高中数学 来源： 题型：
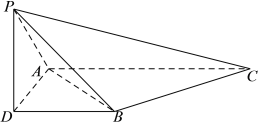
【题目】如图，三棱锥
，侧棱
，底面三角形
为正三角形，边长为
，顶点
在平面
上的射影为
，有
，且
.
（Ⅰ）求证： 
平面
；
（Ⅱ）求二面角
的余弦值；
（Ⅲ）线段
上是否存在点
使得
⊥平面
，如果存在，求
的值；如果不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}的前n项和Sn=2n+1，（n∈N*）．
（1）求数列{an}的通项an；
（2）设bn=nan+1 ， 求数列{bn}的前n项和Tn；
（3）设cn= 
，求证：c1+c2+…+cn＜ 
．（n∈N*）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某中学举行了一次“环保知识竞赛”活动．为了了解本次竞赛学生成绩情况，从中抽取了部分学生的分数（得分取正整数，满分为100分）作为样本（样本容量为n）进行统计．按照
，
，
，
，
的分组作出频率分布直方图，并作出样本分数的茎叶图（图中仅列出了得分在，的数据）．
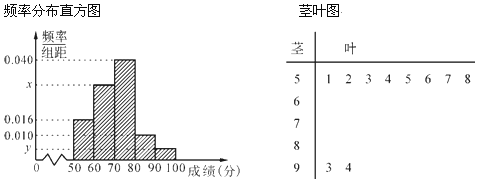
（1）求样本容量n和频率分布直方图中x、y的值;
（2）在选取的样本中，从竞赛成绩是80分以上（含80分）的同学中随机抽取2名同学到市政广场参加环保知识宣传的志愿者活动，求所抽取的2名同学来自不同组的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=ex+2ax（a为常数）的图象与y轴交于点A，曲线y=f（x）在点A处的切线斜率为﹣1．
（1）求a的值及函数f（x）的极值；
（2）证明：当x＞0时，x2+1＜ex ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
