
【题目】已知函数![]() ,其中
,其中![]() 且
且![]() .
.
(1)判断函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)证明:当![]() 时,函数
时,函数![]() 在
在![]() 上为减函数;
上为减函数;
(3)求函数![]() 的值域.
的值域.
 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:
【题目】一个袋中有7个大小、形状相同的小球,6个白球1个红球.现任取1个,若为红球就停止,若为白球就放回,搅拌均匀后再接着取.试设计一个模拟试验,计算恰好第三次摸到红球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017届安徽百校论坛高三文上学期联考二】已知函数![]() .
.
(1)若![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)是否存在整数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上存在极小值,若存在,求出所有整数
上存在极小值,若存在,求出所有整数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,以坐标原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,已知曲线
轴的非负半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,它在点
,它在点![]() 处的切线为直线
处的切线为直线![]() .
.
(Ⅰ)求直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知点![]() 为椭圆
为椭圆![]() 上一点,求点
上一点,求点![]() 到直线
到直线![]() 的距离的取值范围.
的距离的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
在平面直角坐标系中,有三个点的坐标分别是![]() .
.
(1)证明:A,B,C三点不共线;
(2)求过A,B的中点且与直线![]() 平行的直线方程;
平行的直线方程;
(3)设过C且与AB所在的直线垂直的直线为![]() ,求
,求![]() 与两坐标轴围成的三角形的面积.
与两坐标轴围成的三角形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为集合A,B={x|x<a}.
的定义域为集合A,B={x|x<a}.
(1)求集合A;
(2)若AB,求a的取值范围;
(3)若全集U={x|x≤4},a=-1,求U A及A∩(U B).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场经营一批进价为![]() 元/台的小商品,经调查得知如下数据.若销售价上下调整,销售量和利润大体如下:
元/台的小商品,经调查得知如下数据.若销售价上下调整,销售量和利润大体如下:
销售价( |
|
|
|
|
日销售量( |
|
|
|
|
日销售额( |
| |||
日销售利润( |
|
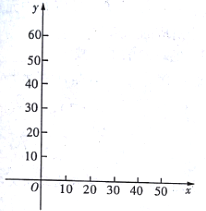
(1)在下面给出的直角坐标系中,根据表中的数据描出实数对![]() 的对应点,并写出
的对应点,并写出![]() 与
与![]() 的一个函数关系式;
的一个函数关系式;
(2)请把表中的空格里的数据填上;
(3)根据表中的数据求![]() 与
与![]() 的函数关系式,并指出当销售单价为多少元时,才能获得最大日销售利润?
的函数关系式,并指出当销售单价为多少元时,才能获得最大日销售利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角A、B、C所对的边分别是a、b、c,向量m=(cos B,cos C),n=(2a+c,b),且m⊥n.
(1)求角B的大小;
(2)若b=![]() ,求a+c的取值范围.
,求a+c的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com