
【题目】某人设计一项单人游戏,规则如下:先将一棋子放在如图所示正方形![]() (边长为3个单位)的顶点
(边长为3个单位)的顶点![]() 处,然后通过掷骰子来确定棋子沿正方形的边按逆时针方向行走的单位,如果掷出的点数为
处,然后通过掷骰子来确定棋子沿正方形的边按逆时针方向行走的单位,如果掷出的点数为![]() ,则棋子就按逆时针方向行走
,则棋子就按逆时针方向行走![]() 个单位,一直循环下去.则某人抛掷三次次骰子后棋子恰好又回到点
个单位,一直循环下去.则某人抛掷三次次骰子后棋子恰好又回到点![]() 处的所有不同走法共有( )
处的所有不同走法共有( )

A.21种B.24种C.25种D.27种
【答案】C
【解析】
抛掷三次骰子后棋子恰好又回到点![]() 处表示三次骰子的点数之和是12,列举出在点数中三个数字能够使得和为12的1,5,6;2,4,6;3,3,6;5,5,2;4,4,4,共有4种组合,前四种组合又可以排列出
处表示三次骰子的点数之和是12,列举出在点数中三个数字能够使得和为12的1,5,6;2,4,6;3,3,6;5,5,2;4,4,4,共有4种组合,前四种组合又可以排列出![]() 种结果,由此利用分类计数原理能得到结果.
种结果,由此利用分类计数原理能得到结果.
由题意知正方形![]() (边长为3个单位)的周长是12,
(边长为3个单位)的周长是12,
抛掷三次骰子后棋子恰好又回到点![]() 处表示三次骰子的点数之和是12,
处表示三次骰子的点数之和是12,
列举出在点数中三个数字能够使得和为12的有1,5,6;2,4,6;3,4,5;3,3,6;5,5,2;4,4,4;共有6种组合,
前三种组合1,5,6;2,4,6;3,4,5;又可以排列出![]() 种结果,
种结果,
3,3,6;5,5,2;有6种结果,4,4,4;有1种结果.
根据分类计数原理知共有![]() 种结果,
种结果,
故选:C.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:
【题目】已知双曲线C:![]() ,O为坐标原点,F为C的右焦点,过F的直线与C的两条渐近线的交点分别为M、N.若
,O为坐标原点,F为C的右焦点,过F的直线与C的两条渐近线的交点分别为M、N.若![]() OMN为直角三角形,则|MN|=
OMN为直角三角形,则|MN|=
A. ![]() B. 3 C.
B. 3 C. ![]() D. 4
D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某度假酒店为了解会员对酒店的满意度,从中抽取50名会员进行调查,把会员对酒店的“住宿满意度”与“餐饮满意度”都分为五个评分标准:1分(很不满意);2分(不满意);3分(一般);4分(满意);5分(很满意).其统计结果如下表(住宿满意度为![]() ,餐饮满意度为
,餐饮满意度为![]() )
)
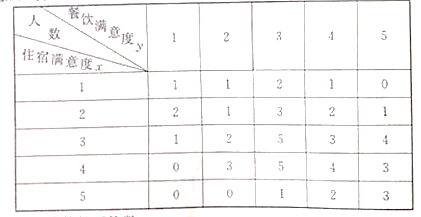
(1)求“住宿满意度”分数的平均数;
(2)求“住宿满意度”为3分时的5个“餐饮满意度”人数的方差;
(3)为提高对酒店的满意度,现从![]() 且
且![]() 的会员中随机抽取2人征求意见,求至少有1人的“住宿满意度”为2的概率.
的会员中随机抽取2人征求意见,求至少有1人的“住宿满意度”为2的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为我国数学家赵爽(约3世纪初)在为《周髀算经》作注时验证勾股定理的示意图,现在提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不相同,则不同的涂色方案共有( )
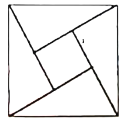
A.360种B.720种C.480种D.420种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解手机品牌的选择是否和年龄的大小有关,随机抽取部分华为手机使用者和苹果机使用者进行统计,统计结果如下表:
年龄 手机品牌 | 华为 | 苹果 | 合计 |
30岁以上 | 40 | 20 | 60 |
30岁以下(含30岁) | 15 | 25 | 40 |
合计 | 55 | 45 | 100 |
附:
P( | 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
根据表格计算得![]() 的观测值
的观测值![]() ,据此判断下列结论正确的是( )
,据此判断下列结论正确的是( )
A.没有任何把握认为“手机品牌的选择与年龄大小有关”
B.可以在犯错误的概率不超过0.001的前提下认为“手机品牌的选择与年龄大小有关”
C.可以在犯错误的概率不超过0.01的前提下认为“手机品牌的选择与年龄大小有关”
D.可以在犯错误的概率不超过0.01
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在国家积极推动美丽乡村建设的政策背景下,各地根据当地生态资源打造了众多特色纷呈的乡村旅游胜地.某人意图将自己位于乡村旅游胜地的房子改造成民宿用于出租,在旅游淡季随机选取100天,对当地已有的六间不同价位的民宿进行跟踪,统计其出租率![]() (
(![]() ),设民宿租金为
),设民宿租金为![]() (单位:元/日),得到如图所示的数据散点图.
(单位:元/日),得到如图所示的数据散点图.

(1)若用“出租率”近似估计旅游淡季民宿每天租出去的概率,求租金为388元的那间民宿在淡季内的三天中至少有2天闲置的概率.
(2)①根据散点图判断,![]() 与
与![]() 哪个更适合于此模型(给出判断即可,不必说明理由)?根据判断结果求回归方程;
哪个更适合于此模型(给出判断即可,不必说明理由)?根据判断结果求回归方程;
②若该地一年中旅游淡季约为280天,在此期间无论民宿是否出租,每天都要付出![]() 的固定成本,若民宿出租,则每天需要再付出
的固定成本,若民宿出租,则每天需要再付出![]() 的日常支出成本.试用①中模型进行分析,旅游淡季民宿租金约定为多少元时,该民宿在这280天的收益
的日常支出成本.试用①中模型进行分析,旅游淡季民宿租金约定为多少元时,该民宿在这280天的收益![]() 达到最大?
达到最大?
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ;
;![]() .
.
参考数据:记![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有长分别为![]() 、
、![]() 、
、![]() 的钢管各3根(每根钢管的质地均匀、粗细相同且富有不同的编号),从中随机抽取
的钢管各3根(每根钢管的质地均匀、粗细相同且富有不同的编号),从中随机抽取![]() 根(假设各钢管被抽取的可能性是均等的,
根(假设各钢管被抽取的可能性是均等的,![]() ),再将抽取的钢管相接焊成笔直的一根.
),再将抽取的钢管相接焊成笔直的一根.
(I)当![]() 时,记事件
时,记事件![]() ,求
,求![]() ;
;
(II)当![]() 时,若用
时,若用![]() 表示新焊成的钢管的长度(焊接误差不计),求
表示新焊成的钢管的长度(焊接误差不计),求![]() 的分布列和数学期望
的分布列和数学期望![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线l过曲线C:y![]() x2的焦点F,并与曲线C交于A(x1,y1),B(x2,y2)两点.
x2的焦点F,并与曲线C交于A(x1,y1),B(x2,y2)两点.
(1)求证:x1x2=﹣16;
(2)曲线C分别在点A,B处的切线(与C只有一个公共点,且C在其一侧的直线)交于点M,求点M的轨迹.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com