【题目】△ABC的内角A，B，C的对边分别为a，b，c，已知sinB+sinA（sinC﹣cosC）=0，a=2，c= 
，则C=（ ）
A.
B.
C.
D.
【答案】B
【解析】解：sinB=sin（A+C）=sinAcosC+cosAsinC，
∵sinB+sinA（sinC﹣cosC）=0，
∴sinAcosC+cosAsinC+sinAsinC﹣sinAcosC=0，
∴cosAsinC+sinAsinC=0，
∵sinC≠0，
∴cosA=﹣sinA，
∴tanA=﹣1，
∵0＜A＜π，
∴A= 
，
由正弦定理可得 
= 
，
∴sinC= 
，
∵a=2，c= 
，
∴sinC= = 
= 
，
∵a＞c，
∴C= 
，
故选：B．
【考点精析】本题主要考查了两角和与差的正弦公式和正弦定理的定义的相关知识点，需要掌握两角和与差的正弦公式：
；正弦定理:
才能正确解答此题．
科目：高中数学 来源： 题型：
【题目】在四棱锥S-ABCD中，底面ABCD是边长为1的正方形，SD
底面ABCD,SD=2，其中
分别是
的中点，
是
上的一个动点．
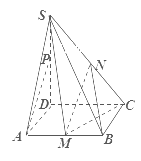
(1)当点落在什么位置时，
∥平面
，证明你的结论；
(2)求三棱锥
的体积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知集合A={x|x＜2}，B={x|3﹣2x＞0}，则（ ）
A.A∩B={x|x＜ 
}
B.A∩B=?
C.A∪B={x|x＜ }
D.AUB=R
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】袋中装有红球3个、白球2个、黑球1个，从中任取2个，则互斥而不对立的两个事件是
A. 至少有一个白球；都是白球 B. 至少有一个白球；至少有一个红球
C. 至少有一个白球；红、黑球各一个 D. 恰有一个白球；一个白球一个黑球
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】△ABC的内角A，B，C的对边分别为a，b，c，已知sin（A+C）=8sin2 
．
（Ⅰ）求cosB；
（Ⅱ）若a+c=6，△ABC面积为2，求b．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】袋中有大小、形状相同的红、黑球各一个，现一次有放回地随机摸取3次，每次摸取一个球
（I）试问：一共有多少种不同的结果？请列出所有可能的结果；
（Ⅱ）若摸到红球时得2分，摸到黑球时得1分，求3次摸球所得总分为5的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
