
【题目】已知函数![]() 在其定义域内有两个不同的极值点.
在其定义域内有两个不同的极值点.
(1)求![]() 的取值范围;
的取值范围;
(2)设两极值点分别为![]() ,
,![]() ,且
,且![]() ,证明:
,证明:![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)对函数进行求导,根据题意可知方程![]() 在
在![]() 上有两个不同的实数根,可以转化为两个函数图象的交点的个数问题,构造新函数,对新函数进行求导,判断其单调性及极值进行求解即可;
上有两个不同的实数根,可以转化为两个函数图象的交点的个数问题,构造新函数,对新函数进行求导,判断其单调性及极值进行求解即可;
(2)要证![]() 成立,只需证
成立,只需证![]() 成立,结合(1),即证
成立,结合(1),即证![]() 成立,利用换元法,构造新函数,对新函数进行求导,根据新函数的单调性进行证明即可.
成立,利用换元法,构造新函数,对新函数进行求导,根据新函数的单调性进行证明即可.
(1)∵函数![]() 的定义域为
的定义域为![]() ,
,
∴方程![]() 在
在![]() 上有两个不同的实数根,
上有两个不同的实数根,
即函数![]() 与
与![]() 的图象在
的图象在![]() 上有两个不同的交点.
上有两个不同的交点.
又∵![]() ,∴当
,∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
故函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
∴![]() 极大值
极大值![]() .
.
又∵![]() 有且只有一个零点1,且当
有且只有一个零点1,且当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
∴要想函数![]() 与函数
与函数![]() 的图象在
的图象在![]() 上有两个不同的交点,只需
上有两个不同的交点,只需![]() .
.
(2)∵要证![]() 成立,∴只需证
成立,∴只需证![]() 成立,
成立,
∵由(1)知![]() ,
,![]() 是方程
是方程![]() 的两个根,即
的两个根,即![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
又∵![]() ,
,![]() ,作差得
,作差得![]() ,即
,即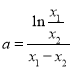 ,
,
∴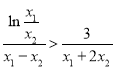 ,∴当
,∴当![]() 时,要证
时,要证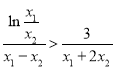 成立,
成立,
即证![]() 成立,令
成立,令![]() ,
,![]() ,
,
即证![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,∴
,∴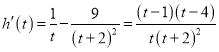 ,
,
∴当![]() 时,
时,![]() ,∴函数
,∴函数![]() 在
在![]() 上单调递增,
上单调递增,
又∵![]() ,∴
,∴![]() ,在
,在![]() 上恒成立,
上恒成立,
∴原不等式成立,即当![]() 时,
时,![]() 成立.
成立.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
【题目】![]() 时代悄然来临,为了研究中国手机市场现状,中国信通院统计了2019年手机市场每月出货量以及与2018年当月同比增长的情况,得到如下统计图,根据该统计图,下列说法错误的是( )
时代悄然来临,为了研究中国手机市场现状,中国信通院统计了2019年手机市场每月出货量以及与2018年当月同比增长的情况,得到如下统计图,根据该统计图,下列说法错误的是( )
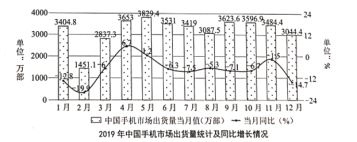
A.2019年全年手机市场出货量中,5月份出货量最多
B.2019年下半年手机市场各月份出货量相对于上半年各月份波动小
C.2019年全年手机市场总出货量低于2018年全年总出货量
D.2018年12月的手机出货量低于当年8月手机出货量
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)为奇函数,且当x≥0时,f(x)=ex﹣cosx,则不等式f(2x﹣1)+f(x﹣2)>0的解集为( )
A.(﹣∞,1)B.(﹣∞,![]() )C.(
)C.(![]() ,+∞)D.(1,+∞)
,+∞)D.(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国有四大国粹:京剧、武术、中医和书法.某大学开设这四门课供学生选修,男生甲选其中三门课进行学习,已知他选修了京剧,则他选修书法的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com