
【题目】已知点![]() 在曲线
在曲线![]() 上,⊙
上,⊙![]() 过原点
过原点![]() ,且与
,且与![]() 轴的另一个交点为
轴的另一个交点为![]() ,若线段
,若线段![]() ,⊙
,⊙![]() 和曲线
和曲线![]() 上分别存在点
上分别存在点![]() 、点
、点![]() 和点
和点![]() ,使得四边形
,使得四边形![]() (点
(点![]() ,
, ![]() ,
, ![]() ,
, ![]() 顺时针排列)是正方形,则称点
顺时针排列)是正方形,则称点![]() 为曲线
为曲线![]() 的“完美点”.那么下列结论中正确的是( ).
的“完美点”.那么下列结论中正确的是( ).
A. 曲线![]() 上不存在”完美点”
上不存在”完美点”
B. 曲线![]() 上只存在一个“完美点”,其横坐标大于
上只存在一个“完美点”,其横坐标大于![]()
C. 曲线![]() 上只存在一个“完美点”,其横坐标大于
上只存在一个“完美点”,其横坐标大于![]() 且小于
且小于![]()
D. 曲线![]() 上存在两个“完美点”,其横坐标均大于
上存在两个“完美点”,其横坐标均大于![]()
科目:高中数学 来源: 题型:
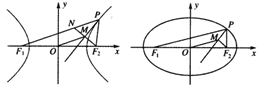
【题目】如图,P是双曲线![]() (a>0,b>0,xy≠0)上的动点,F1,F2是双曲线的焦点,M是∠F1PF2的平分线上一点,且
(a>0,b>0,xy≠0)上的动点,F1,F2是双曲线的焦点,M是∠F1PF2的平分线上一点,且![]() .某同学用以下方法研究|OM|:延长F2M交PF1于点N,可知△PNF2为等腰三角形,且M为F2N的中点,得|OM|=
.某同学用以下方法研究|OM|:延长F2M交PF1于点N,可知△PNF2为等腰三角形,且M为F2N的中点,得|OM|=![]() |NF1|=…=a。类似地:P是椭圆
|NF1|=…=a。类似地:P是椭圆![]() (a>b>0,xy≠0)上的动点,F1,F2是椭圆的焦点,M是∠F1PF2的平分线上一点,且
(a>b>0,xy≠0)上的动点,F1,F2是椭圆的焦点,M是∠F1PF2的平分线上一点,且![]() ,则|OM|的取值范围是________.
,则|OM|的取值范围是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】编号分别为![]() 的16名篮球运动员在某次训练比赛中的得分记录如下:
的16名篮球运动员在某次训练比赛中的得分记录如下:
运动员编号 |
|
|
|
|
|
|
|
|
得分 | 15 | 35 | 21 | 28 | 25 | 36 | 18 | 34 |
运动员编号 |
|
|
|
|
|
|
|
|
得分 | 17 | 26 | 25 | 33 | 22 | 12 | 31 | 38 |
(1)将得分在对应区间内的人数填入相应的空格:
区间 | [10,20) | [20,30) | [30,40] |
人数 |
(2)从得分在区间[20,30)内的运动员中随机抽取2人.
(ⅰ)用运动员编号列出所有可能的抽取结果;
(ⅱ)求这2人得分之和大于50的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的中心在坐标原点![]() ,焦点在
,焦点在![]() 轴上,短轴长为
轴上,短轴长为![]() ,且两个焦点和短轴的两个端点恰为一个正方形的顶点,过右焦点
,且两个焦点和短轴的两个端点恰为一个正方形的顶点,过右焦点![]() 与
与![]() 轴不垂直的直线交椭圆于
轴不垂直的直线交椭圆于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆的方程.
(Ⅱ)当直线![]() 的斜率为
的斜率为![]() 时,求
时,求![]() 的面积.
的面积.
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得经
,使得经![]() ,
, ![]() 为领边的平行四边形是菱形?若存在,求出
为领边的平行四边形是菱形?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着共享单车的成功运营,更多的共享产品逐步走入大家的世界,共享汽车、共享篮球、共享充电宝等各种共享产品层出不穷.某公司随机抽取1000人对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的1000人中的性别以及意见进行了分类,得到的数据如下表所示:
男 | 女 | 总计 | |
认为共享产品对生活有益 | 400 | 300 | 700 |
认为共享产品对生活无益 | 100 | 200 | 300 |
总计 | 500 | 500 | 1000 |
(1)根据表中的数据,能否在犯错误的概率不超过0.1%的前提下,认为共享产品的态度与性别有关系?
(2)为了答谢参与问卷调查的人员,该公司对参与本次问卷调查的人员随机发放1张超市的购物券,购物券金额以及发放的概率如下:
购物券金额 | 20元 | 50元 |
概率 |
|
|
现有甲、乙两人领取了购物券,记两人领取的购物券的总金额为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式: 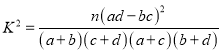 .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市小型机动车驾照“科二”考试中共有5项考察项目,分别记作①,②,③,④,⑤.
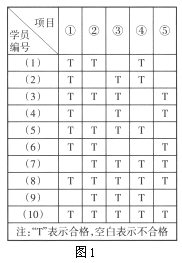
(1)某教练将所带10名学员“科二”模拟考试成绩进行统计(如图1所示),并打算从恰有2项成绩不合格的学员中任意抽出2人进行补测(只测不合格的项目),求补测项目种类不超过3项的概率;
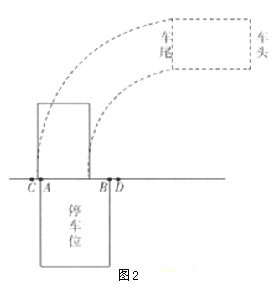
(2)如图2,某次模拟演练中,教练要求学员甲倒车并转向90°,在汽车边缘不压射线AC与射线BD的前提下,将汽车驶入指定的停车位. 根据经验,学员甲转向90°后可使车尾边缘完全落在线段CD,且位于CD内各处的机会相等.若CA="BD=0.3m," AB="2.4m." 汽车宽度为1.8m, 求学员甲能按教练要求完成任务的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com