分析:法一:(Ⅰ)如图,连接CA
1、AC
1、CM,要证CD⊥平面BDM,只需证明直线CD垂直平面BDM内两条相交直线A
1B、DM即可;
(Ⅱ)设F、G分别为BC、BD的中点,连接B
1G、FG、B
1F,说明∠B
1GF
是所求二面角的平面角,然后解三角形,求面B
1BD与面CBD所成二面角的大小.
法二:(Ⅰ)建立空间直角坐标系,求出相关向量计算
•=0,•=0即得证,
(Ⅱ)求出面B
1BD与面CBD的法向量,利用向量的数量积求解可得答案.
解答: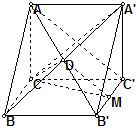
解:法一:(I)如图,连接CA
1、AC
1、CM,则CA
1=
,
∵CB=CA
1=
,∴△CBA
1为等腰三角形,
又知D为其底边A
1B的中点,∴CD⊥A
1B,
∵A
1C
1=1,C
1B
1=
,∴A
1B
1=
,
又BB
1=1,∴A
1B=2,
∵△A
1CB为直角三角形,D为A
1B的中点,CD=
A
1B=1,CD=CC
1.
又DM=
AC
1=
,DM=C
1M,∴△CDN≌△CC
1M,∠CDM=∠CC
1M=90°,即CD⊥DM,
因为A
1B、DM为平面BDM内两条相交直线,所以CD⊥平面BDM.
(II)设F、G分别为BC、BD的中点,连接B
1G、FG、B
1F,
则FG∥CD,FG=
CD.∴FG=
,FG⊥BD.
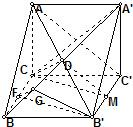
由侧面矩形BB
1A
1A的对角线的交点为D,知BD=B
1D=
A
1B=1,
所以△BB
1D是边长为1的正三角形,于是B
1G⊥BD,B
1G=
,
∴∠B
1GF是所求二面角的平面角.
又B
1F
2=B
1B
2+BF
2=1+(
)
2=
.
∴cos∠B
1GF=
==-.
即所求二面角的大小为π-arccos
.
法二:如图以C为原点建立坐标系.
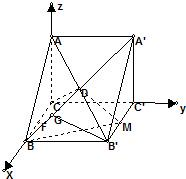
(I)B(
,0,0),B
1(
,1,0),A
1(0,1,1),D(
,
,
),
M(
,1,0),
=(
,
,
),
=(
,-1,-1),
=(0,
,-
),
•=0,•=0,
∴CD⊥A
1B,CD⊥DM.
因为A
1B、DM为平面BDM内两条相交直线,
所以CD⊥平面BDM.
(II)设BD中点为G,连接B
1G,
则G
(,,),
=(-
,
,
),
=
(-,-,),
∴
•=0,∴BD⊥B
1G,
又CD⊥BD,∴
与
的夹角θ等于所求二面角的平面角,
cos
θ==-.所以所求二面角的大小为π-arccos
.
点评:本题考查直线与平面的垂直判定,二面角的求法,考查空间想象能力,逻辑思维能力,是中档题.

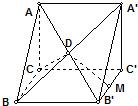 如图,直三棱柱ABC-A1B1C1中,∠ACB=90o,AC=1,CB=
如图,直三棱柱ABC-A1B1C1中,∠ACB=90o,AC=1,CB= 解:法一:(I)如图,连接CA1、AC1、CM,则CA1=
解:法一:(I)如图,连接CA1、AC1、CM,则CA1=
 (I)B(
(I)B(

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=1,CB=
如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=1,CB= 如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点.
如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点. 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点. 如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.
如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.