
分析 (1)利用向量方法,证明$\overrightarrow{AC}∥\overrightarrow{BC}$,即可证明点A,C,B共线;
(2)若$\overrightarrow{AQ}=λ\overrightarrow{QB}({λ∈R})$,当$\overrightarrow{OQ}•\overrightarrow{AB}=0$时,$\overrightarrow{OQ}•\overrightarrow{CQ}=0$,即可求动点Q的轨迹方程.
解答 (1)证明:设$A({t_1^2,{t_1}}),B({t_2^2,{t_2}}),({{t_1}≠{t_2},{t_1}≠0,{t_2}≠0})$,则$\overrightarrow{OA}=({t_1^2,{t_1}}),\overrightarrow{OB}({t_2^2,{t_2}})$,
因为$\overrightarrow{OA}•\overrightarrow{OB}=0$,∴$t_1^2t_2^2+{t_1}{t_2}=0$,又t2≠0,t1≠0,∴t1t2=-1,
因为$\overrightarrow{AC}=({1-t_1^2,-{t_1}}),\overrightarrow{BC}=({1-t_2^2,-{t_2}})$,
且${t_1}({1-t_1^2})-{t_2}({1-t_2^2})=({{t_1}-{t_2}})-{t_1}t_1^2+{t_2}t_2^2=({{t_1}-{t_2}})({1+{t_1}{t_2}})=0$,
所以$\overrightarrow{AC}∥\overrightarrow{BC}$,
又AC,CB都过点C,所以三点A,B,C共线.
(2)解:由题意知,点Q是直角三角形AOB斜边上的垂足,又定点C在直线AB上,∠CQO=90°,
所以设动点Q(x,y),则$\overrightarrow{OQ}=({x,y}),\overrightarrow{CQ}=({x-1,y})$,
又$\overrightarrow{OQ}•\overrightarrow{CQ}=0$,所以x(x-1)+y2=0,即${({x-\frac{1}{2}})^2}+{y^2}=\frac{1}{4}({x≠0})$,
动点Q的轨迹方程为${({x-\frac{1}{2}})^2}+{y^2}=\frac{1}{4}({x≠0})$.
点评 本题考查轨迹方程,考查三点共线的证明,考查向量知识的运用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
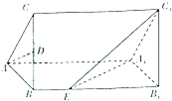 如图,在直棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=$\sqrt{2}$,AA1=3,D是BC的中点,点E在棱BB1上
如图,在直棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=$\sqrt{2}$,AA1=3,D是BC的中点,点E在棱BB1上查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{4}{7}$ | D. | $\frac{5}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com