
【题目】甲、乙二人进行一次围棋比赛,每局胜者得1分,负者得0分,约定一方比另一方多3分或满9局时比赛结束,并规定:只有一方比另一方多三分才算赢,其它情况算平局,假设在每局比赛中,甲获胜的概率为![]() ,乙获胜的概率为
,乙获胜的概率为![]() ,各局比赛结果相互独立,已知前3局中,甲胜2局,乙胜1局.
,各局比赛结果相互独立,已知前3局中,甲胜2局,乙胜1局.
(1) 求甲获得这次比赛胜利的概率;
(2)设![]() 表示从第4局开始到比赛结束所进行的局数,求
表示从第4局开始到比赛结束所进行的局数,求![]() 得分布列及数学期望.
得分布列及数学期望.
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() :
: ![]()
![]() 的焦距与椭圆
的焦距与椭圆![]() :
: ![]() 的短轴长相等,且
的短轴长相等,且![]() 与
与![]() 的长轴长相等,这两个椭圆在第一象限的交点为
的长轴长相等,这两个椭圆在第一象限的交点为![]() ,直线
,直线![]() 经过
经过![]() 在
在![]() 轴正半轴上的顶点
轴正半轴上的顶点![]() 且与直线
且与直线![]() (
(![]() 为坐标原点)垂直,
为坐标原点)垂直, ![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,
, ![]() 与
与![]() 交于
交于![]() ,
, ![]() 两点.
两点.
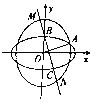
(1)求![]() 的标准方程;
的标准方程;
(2)求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
袋中有形状和大小完全相同的四种不同颜色的小球,每种颜色的小球各有4个,分别编号为1,2,3,4.现从袋中随机取两个球.
(Ⅰ)若两个球颜色不同,求不同取法的种数;
(Ⅱ)在(1)的条件下,记两球编号的差的绝对值为随机变量X,求随机变量X的概率分布与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】吸烟有害健康,远离烟草,珍惜生命。据统计一小时内吸烟5支诱发脑血管病的概率为0.02,一小时内吸烟10支诱发脑血管病的概率为0.16.已知某公司职员在某一小时内吸烟5支未诱发脑血管病,则他在这一小时内还能继吸烟5支不诱发脑血管病的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 不确定
D. 不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于回归分析的说法中错误的是( )
A. 回归直线一定过样本中心![]()
B. 残差图中残差点比较均匀地落在水平的带状区域中,说明选用的模型比较合适
C. 两个模型中残差平方和越小的模型拟合的效果越好
D. 甲、乙两个模型的![]() 分别约为0.98和0.80,则模型乙的拟合效果更好
分别约为0.98和0.80,则模型乙的拟合效果更好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,点P(1,
,点P(1,![]() )在椭圆C上,直线l过椭圆的右焦点与椭圆相交于A,B两点.
)在椭圆C上,直线l过椭圆的右焦点与椭圆相交于A,B两点.
(1)求椭圆C的方程;
(2)在x轴上是否存在定点M,使得![]() 为定值?若存在,求定点M的坐标;若不在,请说明理由.
为定值?若存在,求定点M的坐标;若不在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com