
【题目】已知定义在区间![]() 上的函数
上的函数![]() ,其中常数
,其中常数![]() .
.
(1)若函数![]() 分别在区间
分别在区间![]() 上单调,试求
上单调,试求![]() 的取值范围;
的取值范围;
(2)当![]() 时,方程
时,方程![]() 有四个不相等的实根
有四个不相等的实根![]() .
.
①证明: ![]() ;
;
②是否存在实数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 单调,且
单调,且![]() 的取值范围为
的取值范围为![]() ,若存在,求出
,若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(1) ![]() (2)见解析,
(2)见解析, ![]()
【解析】试题分析:(1)结合对勾函数的特征,即可知![]() ,从而求出参数范围;(2)当
,从而求出参数范围;(2)当![]() 时,方程
时,方程![]() 即为
即为![]() 或
或![]() ,由韦达定理可证明.结合函数图像及其单调性,分类讨论分别在四个单调区间内去求解,最后求并集即可.
,由韦达定理可证明.结合函数图像及其单调性,分类讨论分别在四个单调区间内去求解,最后求并集即可.
试题解析:(1)设![]()
∵![]() ∴函数
∴函数![]() 分别在区间
分别在区间![]() 上单调 且
上单调 且![]()
要使函数![]() 分别在区间
分别在区间![]() 上单调
上单调
则只需![]()
(2)①当![]() 时,
时, ![]() 或
或![]()
即![]() 或
或![]()
∵![]() 为方程
为方程![]() 的四个不相等的实根
的四个不相等的实根
∴由根与系数的关系得![]()
②如图,可知![]() ,
, ![]() 在
在![]() 、
、![]() 、
、![]() 、
、![]() 均为单调函数
均为单调函数
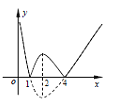
(Ⅰ)当![]() 时,
时, ![]() 在
在![]() 上单调递减
上单调递减
则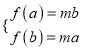 两式相除整理得
两式相除整理得![]()
∵![]() ∴上式不成立 即
∴上式不成立 即![]() 无解,
无解, ![]() 无取值 10分
无取值 10分
(Ⅱ)当![]() 时,
时, ![]() 在
在![]() 上单调递增
上单调递增
则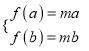 即
即![]() 在
在![]() 有两个不等实根
有两个不等实根
而令![]() 则
则![]()
作![]() 在
在![]() 的图像可知,
的图像可知, ![]() 12分
12分
(Ⅲ)当![]() 时,
时, ![]() 在
在![]() 上单调递减
上单调递减
则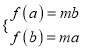 两式相除整理得
两式相除整理得![]()
∴![]() ∴
∴![]() ∴
∴![]()
由![]() 得
得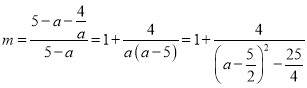
则![]() 关于
关于![]() 的函数是单调的,而
的函数是单调的,而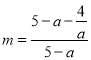 应有两个不同的解
应有两个不同的解
∴此种情况无解
(Ⅳ)当![]() 时,同(Ⅰ)可以解得
时,同(Ⅰ)可以解得![]() 无取值
无取值
综上, ![]() 的取值范围为
的取值范围为![]()


科目:高中数学 来源: 题型:
【题目】某保险公司有一款保险产品的历史收益率(收益率![]() 利润
利润![]() 保费收入)的频率分布直方图如图所示:
保费收入)的频率分布直方图如图所示:
(1)试估计这款保险产品的收益率的平均值;
(2)设每份保单的保费在20元的基础上每增加![]() 元,对应的销量为
元,对应的销量为![]() (万份).从历史销售记录中抽样得到如下5组
(万份).从历史销售记录中抽样得到如下5组![]() 与
与![]() 的对应数据:
的对应数据:
| 25 | 30 | 38 | 45 | 52 |
销量为 | 7.5 | 7.1 | 6.0 | 5.6 | 4.8 |
由上表,知![]() 与
与![]() 有较强的线性相关关系,且据此计算出的回归方程为
有较强的线性相关关系,且据此计算出的回归方程为![]() .
.

(ⅰ)求参数![]() 的值;
的值;
(ⅱ)若把回归方程![]() 当作
当作![]() 与
与![]() 的线性关系,用(1)中求出的收益率的平均值作为此产品的收益率,试问每份保单的保费定为多少元时此产品可获得最大利润,并求出最大利润.注:保险产品的保费收入
的线性关系,用(1)中求出的收益率的平均值作为此产品的收益率,试问每份保单的保费定为多少元时此产品可获得最大利润,并求出最大利润.注:保险产品的保费收入![]() 每份保单的保费
每份保单的保费![]() 销量.
销量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() 满足:
满足:![]() 对任意
对任意![]() 、
、![]()
![]() 恒成立,当
恒成立,当![]() 时,
时,![]() .
.
(1)求证![]() 在
在![]() 上是单调递增函数;
上是单调递增函数;
(2)已知![]() ,解关于
,解关于![]() 的不等式
的不等式![]() ;
;
(3)若![]() ,且不等式
,且不等式![]() 对任意
对任意![]() 恒成立.求实数
恒成立.求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】吉安一中举行了一次“环保知识竞赛”活动,为了解本了次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为![]() 分)作为样本(样本容量为
分)作为样本(样本容量为![]() )进行统计. 按照
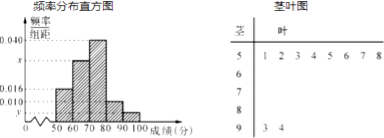
)进行统计. 按照 ![]() 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在![]() 的数据).
的数据).
(1)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(2)在选取的样本中,从竞赛学生成绩是![]() 分以上(含
分以上(含![]() 分)的同学中随机抽取
分)的同学中随机抽取![]() 名同学到市政广场参加环保知识宣传的志愿者活动,设
名同学到市政广场参加环保知识宣传的志愿者活动,设![]() 表示所抽取的
表示所抽取的![]() 名同学中得分在
名同学中得分在![]() 的学生人数,求
的学生人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)满足f(x)=f(x+4),当2≤x≤6时, ![]() ,f(4)=31.
,f(4)=31.
(1)求m,n的值;
(2)比较f(log3m)与f(log3n)的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分) 函数f(x)是定义在R上的偶函数,已知当x≤0时,f(x)=x2+4x+3.
(1)求函数f(x)的解析式;
(2)画出函数的图象,并写出函数f(x)的单调区间;
(3)求f(x)在区间[-1,2]上的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com