
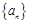 的前n项和为Sn,已知
的前n项和为Sn,已知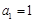 ,且
,且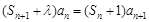 对一切
对一切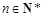 都成立.
都成立.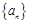 的通项公式;
的通项公式;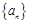 是等差数列.
是等差数列.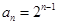 ;(2)
;(2)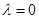 .
.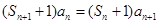 ,我们要从这个式子想办法得出
,我们要从这个式子想办法得出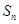 与
与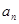 的简单关系式,变形为
的简单关系式,变形为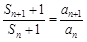 ,这时我们联想到累乘法求数列通项公式的题型,因此首先由
,这时我们联想到累乘法求数列通项公式的题型,因此首先由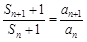 得
得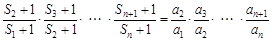 ,又
,又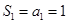 ,这个式子可化简为
,这个式子可化简为 ,这样就变成我们熟悉的已知条件,已知解法了;(2)这种类型问题,一种方法是从特殊到一般的方法,可由
,这样就变成我们熟悉的已知条件,已知解法了;(2)这种类型问题,一种方法是从特殊到一般的方法,可由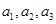 成等差数列,求出
成等差数列,求出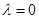 ,然后把
,然后把
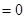 代入已知等式,得
代入已知等式,得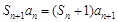 ,
, ,这个等式比第(1)题难度大点,把
,这个等式比第(1)题难度大点,把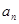 化为
化为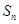 ,有当n≥2时,
,有当n≥2时,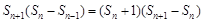 ,整理,得
,整理,得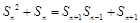 ,特别是可变形为
,特别是可变形为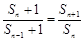 ,这样与第(1)处理方法相同,可得
,这样与第(1)处理方法相同,可得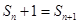 ,即
,即 ,从而说不得
,从而说不得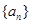 是等差数列.
是等差数列. 试题解析:(1)若λ=1,则
试题解析:(1)若λ=1,则 ,
, .
.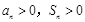 ,∴
,∴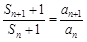 , 2分
, 2分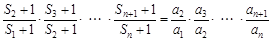 ,
,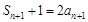 .① 4分
.① 4分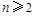 时,
时,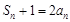 .②
.②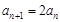 ,∴
,∴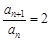 (
(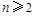 ). 6分
). 6分 ,∴n=1时上式也成立,
,∴n=1时上式也成立,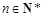 ). 8分
). 8分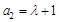 .令n=2,得
.令n=2,得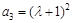 . 10分
. 10分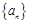 是等差数列,必须有
是等差数列,必须有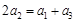 ,解得λ=0. 11分
,解得λ=0. 11分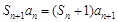 ,且
,且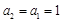 .
.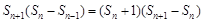 ,
,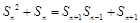 ,
,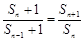 , 13分
, 13分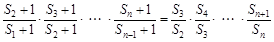 ,
,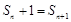 ,所以
,所以 . 15分
. 15分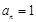 (
(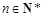 ),
),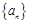 是等差数列. 16分
是等差数列. 16分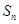 与
与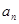 的关系,等差数列.
的关系,等差数列.

科目:高中数学 来源:不详 题型:解答题
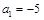 ,
,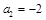 ,记
,记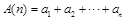 ,
,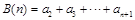 ,
,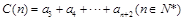 ,若对于任意
,若对于任意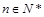 ,A(n),B(n),C(n)成等差数列.
,A(n),B(n),C(n)成等差数列.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.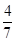 尺 尺 | B.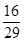 尺 尺 | C.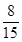 尺 尺 | D.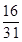 尺 尺 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com