练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知曲线： ， ： （），从上的点作轴的垂线，交于点，再从点作轴的垂线，交于点.设， ， .

    （Ⅰ）求数列的通项公式；

    （Ⅱ）记，数列的前项和为，求证： ；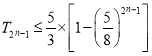

    （Ⅲ）若已知（），记数列的前项和为，数列的前项和为，试比较与的大小.

    【答案】（1） ；（2）见解析；（3）见解析.

    【解析】试题分析：（1）依题意点的坐标为，则∴

    从而能求出数列的通项公式．
    （2）由，知，，当时， ，∴ ．由此能够证明；

    （3）由∵，∴，由知（）

    ∴（），而，所以可得，

    由此能够比较与的大小．

    试题解析：（1）依题意点的坐标为，

    ∴∴

    ∴

    .

    （2）∵，所以： ，

    ∴当时， ，

    ∴ （当时取“”）.

    （Ⅲ）∵，∴，

    由知（）

    ∴（），而，所以可得，

    于是

    .

    ∴

    当， 时， ；

    当时，

    当时，

    ∴当时，

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，内角A，B，C的对边分别为a，b，c．已知 ．
    （1）求 的值；
    （2）若cosB= ，△ABC的周长为5，求b的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为研究患肺癌与是否吸烟有关，做了一次相关调查，其中部分数据丢失，但可以确定的是不吸烟人数与吸烟人数相同，吸烟患肺癌人数占吸烟总人数的；不吸烟的人数中，患肺癌与不患肺癌的比为．

    （1）若吸烟不患肺癌的有人，现从患肺癌的人中用分层抽样的方法抽取人，再从这人中随机抽取人进行调查，求这两人都是吸烟患肺癌的概率；

    （2）若研究得到在犯错误概率不超过的前提下，认为患肺癌与吸烟有关，则吸烟的人数至少有多少？

    附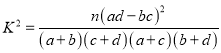： ，其中．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】证明下列不等式：
    （1）设a，b，c∈R* ， 且满足条件a+b+c=1，证明： ≥9
    （2）已知a≥0，证明： ＜ ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一家面包房根据以往某种面包的销售记录，绘制了日销售量的频率分布直方图，如图所示．将日销售量落入各组的频率视为概率．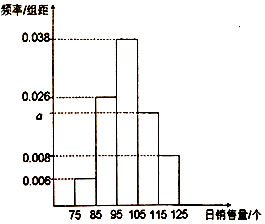

    （1）求a的值并估计在一个月（按30天算）内日销售量不低于105个的天数；
    （2）利用频率分布直方图估计每天销售量的平均值及方差（同一组中的数据用该组区间的中点值作代表）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数（）

    （Ⅰ）当时，求在处的切线方程；

    （Ⅱ）求单调区间；

    （Ⅲ）若图象与轴关于， 两点，求证： .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知单调递减的等比数列{an}满足：a2+a3+a4=28，且a3+2是a2 ， a4是等差中项，则公比q= ， 通项公式为an= ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某人在静水中游泳，速度为4公里/小时，他在水流速度为4公里/小时的河中游泳．
    （1）若他垂直游向河对岸，则他实际沿什么方向前进？实际前进的速度为多少？
    （2）他必须朝哪个方向游，才能沿与水流垂直的方向前进？实际前进的速度为多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在锐角△ABC中，内角A，B，C所对的边分别为a，b，c，已知 a=2csinA．
    （1）求角C的值；
    （2）若c= ，且S△ABC= ，求a+b的值．

    查看答案和解析>>

    同步练习册答案