
【题目】下面给出四种说法:
①设![]() 、
、![]() 、
、![]() 分别表示数据15、17、14、10、15、17、17、16、14、12的平均数、中位数、众数,则
分别表示数据15、17、14、10、15、17、17、16、14、12的平均数、中位数、众数,则![]() ;
;
②在线性回归模型中,相关系数![]() 的绝对值越接近于1,表示两个变量的相关性越强;
的绝对值越接近于1,表示两个变量的相关性越强;
③绘制频率分布直方图时,各小长方形的面积等于相应各组的组距;
④线性回归直线不一定过样本中心点![]() .
.
其中正确说法的序号是______.
【答案】①②
【解析】
对于①根据数据求得平均数、中位数、众数,即可比较![]() 的大小;对于②根据相关系数定义,即可判断是否正确;对于③,根据频率分布直方图的绘制过程即可判断;对于④根据线性回归方程中
的大小;对于②根据相关系数定义,即可判断是否正确;对于③,根据频率分布直方图的绘制过程即可判断;对于④根据线性回归方程中![]() 的求法,可知必过样本中心点
的求法,可知必过样本中心点![]() ,即可判断.
,即可判断.
对于①,根据数据可求得平均数为![]() ,从小到大排列可得
,从小到大排列可得![]() ,所以中位数为
,所以中位数为![]() ,由数据可知众数为
,由数据可知众数为![]() .即
.即![]() ,所以①正确;
,所以①正确;
对于②根据相关系数的意义,可知当相关系数![]() 的绝对值越接近于1,表示两个变量的相关性越强,所以②正确;
的绝对值越接近于1,表示两个变量的相关性越强,所以②正确;
对于③绘制频率分布直方图时,各小长方形的面积等于相应各组的频率,所以③错误;
对于④根据线性回归方程中![]() 的求法,可知必过样本中心点
的求法,可知必过样本中心点![]() ,所以④错误.
,所以④错误.
综上可知,正确的为①②
故答案为: ①②


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:高中数学 来源: 题型:
【题目】有关部门要了解甲型H1N1流感预防知识在学校的普及情况,命制了一份有10道题的问卷到各学校做问卷调查.某中学A、B两个班各被随机抽取5名学生接受问卷调查,A班5名学生得分为:5、8、9、9、9,B班5名学生得分为:6、7、8、9、10.
(1)请你判断A、B两个班中哪个班的问卷得分要稳定一些,并说明你的理由;
(2)求如果把B班5名学生的得分看成一个总体,并用简单随机抽样方法从中抽取样本容量为2的样本,求样本平均数与总体平均数之差的绝对值不小于1的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于四面体ABCD,给出下列四个命题:
①若AB=AC,BD=CD,则BC⊥AD; ②若AB=CD,AC=BD,则BC⊥AD;
③若AB⊥AC,BD⊥CD,则BC⊥AD;④若AB⊥CD,AC⊥BD,则BC⊥AD;
其中正确的命题的序号是( )
A.①②B.②③C.②④D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() .
.
(1)当![]() 时,函数
时,函数![]() 有两个极值点,求
有两个极值点,求![]() 的取值范围;
的取值范围;
(2)若![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴平行,且函数
轴平行,且函数![]() 在
在![]() 时,其图象上每一点处切线的倾斜角均为锐角,求
时,其图象上每一点处切线的倾斜角均为锐角,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区不同身高![]() 的未成年男孩的体重平均值
的未成年男孩的体重平均值![]() 如下表:
如下表:
身高 | 60 | 70 | 80 | 90 | 100 |
体重 | 6.13 | 7.90 | 9.99 | 12.15 | 15.02 |
已知![]() 与
与![]() 之间存在很强的线性相关性,
之间存在很强的线性相关性,
(1)据此建立![]() 与
与![]() 之间的回归方程;
之间的回归方程;
(2)若体重超过相同身高男性体重平均值的1.2倍为偏胖,低于0.8倍为偏瘦,那么这个地区一名身高![]() 体重为
体重为![]() 的在校男生的体重是否正常?
的在校男生的体重是否正常?
参考数据:![]() ,
,![]() ,
,![]()
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计算机在数据处理时使用的是二进制,例如十进制数1,2,3,4的二进制数分别表示为1,10,11,100,二进制数…![]() 化为十进制数的公式为…
化为十进制数的公式为…![]()
![]() ,例如二进制数11等于十进制数
,例如二进制数11等于十进制数![]() ,又如二进制数101等于十进制数
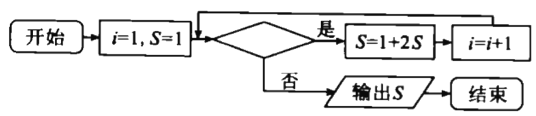
,又如二进制数101等于十进制数![]() ,下图是某同学设计的将二进制数11111化为十进制数的程序框图,则判断框内应填入的条件是( )
,下图是某同学设计的将二进制数11111化为十进制数的程序框图,则判断框内应填入的条件是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是周期为4的奇函数,且当
是周期为4的奇函数,且当![]() 时,
时,![]() ,方程
,方程![]() 在区间
在区间![]() 内有唯一解
内有唯一解![]() ,则方程
,则方程![]() 在区间
在区间![]() 上所有解的和为( )
上所有解的和为( )
A. ![]() B. 036162C. 3053234D. 3055252
B. 036162C. 3053234D. 3055252
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com