
【题目】已知抛物线![]() :
:![]() 过点
过点![]() ,
,![]() 为其焦点,过
为其焦点,过![]() 且不垂直于
且不垂直于![]() 轴的直线
轴的直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,动点
两点,动点![]() 满足
满足![]() 的垂心为原点
的垂心为原点![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)求证:动点![]() 在定直线
在定直线![]() 上,并求
上,并求![]() 的最小值.
的最小值.
【答案】(1)![]() (2)证明见解析,
(2)证明见解析,![]() 的最小值为
的最小值为![]()
【解析】
(1)直接将![]() 代入抛物线方程即可得到答案;
代入抛物线方程即可得到答案;
(2)设直线方程为![]() ,联立方程,表示出
,联立方程,表示出![]() ,运用基本不等式即可得到结论.
,运用基本不等式即可得到结论.
(1)由题意,将点![]() 代入
代入![]() ,
,
即![]() ,解得
,解得![]() ,
,
所以,抛物线![]() 的方程为
的方程为![]() .
.
(2)解析1:(巧设直线)
证明:设![]() :
:![]() ,
,![]() ,
,![]() ,联立
,联立![]() ,可得
,可得![]() ,则有
,则有 ,可设
,可设![]() :
:![]() ,即
,即![]() ,同理
,同理![]() :
:![]() ,解得
,解得![]() ,即动点
,即动点![]() 在定直线
在定直线![]() :
:![]() 上.
上.

![]() ,当且仅当
,当且仅当![]() 时取等号.其中
时取等号.其中![]() ,
,![]() 分别为点
分别为点![]() 和点
和点![]() 到直线
到直线![]() 的距离.
的距离.
(2)解析2:(利用向量以及同构式)
证明:设![]() :
:![]() ,
,![]() ,
,![]() ,联立
,联立![]() ,可得
,可得![]() ,则有
,则有 .
. ,
, ,又
,又![]() 为
为![]() 的垂心,从而
的垂心,从而![]() ,代入化简得:
,代入化简得:![]() ,同理:
,同理:![]() ,从而可知,
,从而可知,![]() ,
,![]() 是方程
是方程![]() 的两根,所以
的两根,所以
 ,所以动点
,所以动点![]() 在定直线
在定直线![]() :
:![]() 上.
上.
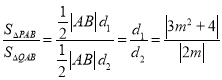
![]() ,当且仅当
,当且仅当![]() 时取等号.其中
时取等号.其中![]() ,
,![]() 分别为点
分别为点![]() 和点
和点![]() 到直线
到直线![]() 的距离.
的距离.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的一个焦点为
的一个焦点为![]() ,离心率为
,离心率为![]() .
.
(1)求![]() 的标准方程;
的标准方程;
(2)若动点![]() 为
为![]() 外一点,且
外一点,且![]() 到
到![]() 的两条切线相互垂直,求
的两条切线相互垂直,求![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)设![]() 的另一个焦点为
的另一个焦点为![]() ,过
,过![]() 上一点
上一点![]() 的切线与(2)所求轨迹
的切线与(2)所求轨迹![]() 交于点
交于点![]() ,
,![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
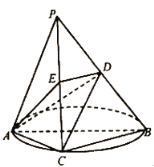
【题目】如图,![]() 是一个三棱锥,
是一个三棱锥,![]() 是圆的直径,
是圆的直径,![]() 是圆上的点,
是圆上的点,![]() 垂直圆所在的平面,
垂直圆所在的平面,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)若二面角![]() 是
是![]() ,
,![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若存在正常数
,若存在正常数![]() ,使得对任意的
,使得对任意的![]() ,都有
,都有![]() 成立,我们称函数
成立,我们称函数![]() 为“
为“![]() 同比不减函数”.
同比不减函数”.
(1)求证:对任意正常数![]() ,
,![]() 都不是“
都不是“![]() 同比不减函数”;
同比不减函数”;
(2)若函数![]() 是“
是“![]() 同比不减函数”,求
同比不减函数”,求![]() 的取值范围;
的取值范围;
(3)是否存在正常数![]() ,使得函数
,使得函数![]() 为“
为“![]() 同比不减函数”,若存在,求
同比不减函数”,若存在,求![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为R的函数![]() ,若函数
,若函数![]() 是奇函数,则称
是奇函数,则称![]() 为正弦奇函数.已知
为正弦奇函数.已知![]() 是单调递增的正弦奇函数,其值域为R,
是单调递增的正弦奇函数,其值域为R,![]() .
.
(1)已知![]() 是正弦奇函数,证明:“
是正弦奇函数,证明:“![]() 为方程
为方程![]() 的解”的充要条件是“
的解”的充要条件是“![]() 为方程
为方程![]() 的解”;
的解”;
(2)若![]()
![]() ,求
,求![]() 的值;
的值;
(3)证明:![]() 是奇函数.
是奇函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且2acosB=2c﹣b.
(1)求∠A的大小;
(2)若△ABC的外接圆的半径为![]() ,面积为
,面积为![]() ,求△ABC的周长.
,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了鼓励职员工作热情,某公司对每位职员一年来的工作业绩按月进行考评打分;年终按照职员的月平均值评选公司最佳职员并给予相应奖励.已知职员![]() 一年来的工作业绩分数的茎叶图如图所示:
一年来的工作业绩分数的茎叶图如图所示:
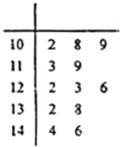
(1)根据职员![]() 的业绩茎叶图求出他这一年的工作业绩的中位数和平均数;
的业绩茎叶图求出他这一年的工作业绩的中位数和平均数;
(2)由于职员![]() 的业绩高,被公司评为年度最佳职员,在公司年会上通过抽奖形式领取奖金.公司准备了六张卡片,其中一张卡片上标注奖金为6千元,两张卡片的奖金为4千元,另外三张的奖金为2千元.规则是:获奖职员
的业绩高,被公司评为年度最佳职员,在公司年会上通过抽奖形式领取奖金.公司准备了六张卡片,其中一张卡片上标注奖金为6千元,两张卡片的奖金为4千元,另外三张的奖金为2千元.规则是:获奖职员![]() 需要从六张卡片中随机抽出两张,这两张卡片上的金额数之和作为奖金数.求职员
需要从六张卡片中随机抽出两张,这两张卡片上的金额数之和作为奖金数.求职员![]() 获得奖金6千元的概率;并说明获得奖金6千元和8千元哪个可能性较大?
获得奖金6千元的概率;并说明获得奖金6千元和8千元哪个可能性较大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{bn}的前n项和为Tn,且T4=4,b5=6.
(1)求数列{bn}的通项公式;
(2)若正整数n1,n2,…,nt,…满足5<n1<n2<…<nt,…且b3,b5,![]() ,
,![]() ,…,
,…,![]() ,…成等比数列,求数列{nt}的通项公式(t是正整数);
,…成等比数列,求数列{nt}的通项公式(t是正整数);
(3)给出命题:在公比不等于1的等比数列{an}中,前n项和为Sn,若am,am+2,am+1成等差数列,则Sm,Sm+2,Sm+1也成等差数列.试判断此命题的真假,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将曲线![]() 上各点的纵坐标伸长为原来的
上各点的纵坐标伸长为原来的![]() 倍(横坐标不变)得到曲线
倍(横坐标不变)得到曲线![]() ,求
,求![]() 的参数方程;
的参数方程;
(2)若![]() ,
,![]() 分别是直线
分别是直线![]() 与曲线
与曲线![]() 上的动点,求
上的动点,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com