
【题目】已知![]() ,函数
,函数![]() 有两个不同的极值点
有两个不同的极值点![]() ,
,![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)证明:![]() .
.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)求函数![]() 的定义域
的定义域![]() ,以及导数
,以及导数![]() ,将问题转化为导数方程
,将问题转化为导数方程
![]() ,转化为二次方程
,转化为二次方程![]() 在
在![]() 上有两个不等的实根,再分析
上有两个不等的实根,再分析![]() 、对称轴以及二次函数
、对称轴以及二次函数![]() 在
在![]() 处函数值的正负,列出有关
处函数值的正负,列出有关![]() 的不等式组解出即可;
的不等式组解出即可;
(2)由![]() 、
、![]() 为二次方程
为二次方程![]() 的两根,列出韦达定理,再将韦达定理代入代数式
的两根,列出韦达定理,再将韦达定理代入代数式![]() ,经过化简得出
,经过化简得出![]() 关于
关于![]() 的函数,并令
的函数,并令![]() ,
,
转化为![]() 关于
关于![]() 的函数,再利用导数结合单调性证明结论成立。
的函数,再利用导数结合单调性证明结论成立。
(1)![]() ,函数
,函数![]() 定义域:
定义域:![]() .,
.,
![]() ,
,
函数![]() 有两个不同的极值点
有两个不同的极值点![]() ,img src="http://thumb.1010pic.com/questionBank/Upload/2020/05/28/06/0c1e6116/SYS202005280601105383817422_DA/SYS202005280601105383817422_DA.012.png" width="18" height="24" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />.对于
,img src="http://thumb.1010pic.com/questionBank/Upload/2020/05/28/06/0c1e6116/SYS202005280601105383817422_DA/SYS202005280601105383817422_DA.012.png" width="18" height="24" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />.对于![]() 中的
中的![]() 应满足①②③三个条件:
应满足①②③三个条件:
![]() ,①,△
,①,△![]() ,②
,②![]() ,③
,③
由①②③可得![]() 的取值范围:
的取值范围:![]() ,
,
(2)证明:![]() ,
,
得:![]() ,
,![]() .
.![]() ,
,
![]()
![]() ,
,
令![]() ,则
,则![]() ,
,
将其令为![]() 即:
即:![]() ,则有:
,则有:![]() ,
,
![]() ,
,![]() ,
,![]() 在定义域是单调递减的函数,
在定义域是单调递减的函数,
![]() (4)
(4)![]() ,
,![]() 在定义域也是单调递减的函数,
在定义域也是单调递减的函数,![]() (4)
(4)![]() .
.
即:![]() 得证.
得证.


科目:高中数学 来源: 题型:
【题目】共有编号分别为1,2,3,4,5的五个座位,在甲同学不坐2号座位,乙同学不坐5号座位的条件下,甲、乙两位同学的座位号相加是偶数的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区甲、乙、丙三所单位进行招聘,其中甲单位招聘2名,乙单位招聘2名,丙单位招聘1名,并且甲单位要至少招聘一名男生,现有3男3女参加三所单位的招聘,则不同的录取方案种数为( )
A.36B.72C.108D.144
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】窗花是贴在窗纸或窗户玻璃上的剪纸,是中国古老的传统民间艺术之一.图中的窗花是由一张圆形纸片剪去一个正十字形剩下的部分,正十字形的顶点都在圆周上.已知正十字形的宽和长都分别为x,y(单位:dm)且x<y,若剪去的正十字形部分面积为4dm2.
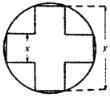
(1)求y关于x的函数解析式,并求其定义域;
(2)现为了节约纸张,需要所用圆形纸片面积最小.当x取何值时,所用到的圆形纸片面积最小,并求出其最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某企业的某种产品中抽取![]() 件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:
件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:
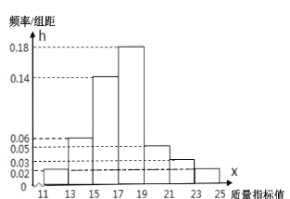
(Ⅰ)求这![]() 件产品质量指标值的样本平均数
件产品质量指标值的样本平均数![]() 和样本方差
和样本方差![]() (同一组数据用该区间的中点值作代表,记作
(同一组数据用该区间的中点值作代表,记作![]() ,
,![]() );
);
(Ⅱ)由频率分布直方图可以认为,这种产品的质量指标值![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(i)若使![]() 的产品的质量指标值高于企业制定的合格标准,则合格标准的质量指标值大约为多少?
的产品的质量指标值高于企业制定的合格标准,则合格标准的质量指标值大约为多少?
(ii)若该企业又生产了这种产品![]() 件,且每件产品相互独立,则这
件,且每件产品相互独立,则这![]() 件产品质量指标值不低于
件产品质量指标值不低于![]() 的件数最有可能是多少?
的件数最有可能是多少?
附:参考数据与公式:![]() ,
,![]() ;若
;若![]() ,则①
,则①![]() ;②
;②![]() ;③
;③![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试立定跳远的成绩用茎叶图表示如图(单位:![]() ):男生成绩在175
):男生成绩在175![]() 以上(包括175
以上(包括175![]() )定义为“合格”,成绩在175
)定义为“合格”,成绩在175![]() 以下(不包括175
以下(不包括175![]() )定义为“不合格”.女生成绩在165
)定义为“不合格”.女生成绩在165![]() 以上(包括165
以上(包括165![]() )定义为“合格”,成绩在165
)定义为“合格”,成绩在165![]() 以下(不包括165
以下(不包括165![]() )定义为“不合格”.
)定义为“不合格”.

(1)求五年一班的女生立定跳远成绩的中位数;
(2)在五年一班的男生中任意选取3人,求至少有2人的成绩是合格的概率;
(3)若从五年一班成绩“合格”的学生中选取2人参加复试,用![]() 表示其中男生的人数,写出
表示其中男生的人数,写出![]() 的分布列,并求
的分布列,并求![]() 的数学期望.
的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com